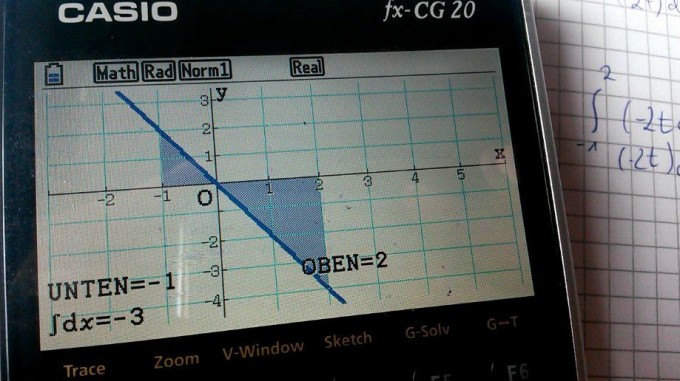
Die Matheaufgabe lautet: Bestimmen Sie das Integral mithilfe von Dreiecks-und Rechtecksflächen.
So, ich verstehe die Aufgabe, bleibe jedoch bei der c) immer hängen:
c)
∫(von -1 bis 2) -2tdt
Wenn ich mit meinem Taschenrechner das Integral berechne, kommt -3 raus.
Und wenn ich es selbst rechne :
linkes Dreieck: -1x2= -2 , -2:2 = -1 also linkes Dreieck: -1
rechtes Dreieck: 2x (-4) = -8 , -8:2= -4 also rechtes Dreieck: -4
wenn ich die beiden Dreiecke addiere kommt aber dann -5 raus ?