Grenzwertberechnung mit Koeffizienten

Question

Hey zusammen! :)

Ich habe diesmal eine ziemlich einfache Aufgabe, allerdings sitze ich ziemlich lange dran und verstehe die Lösung nicht... :

x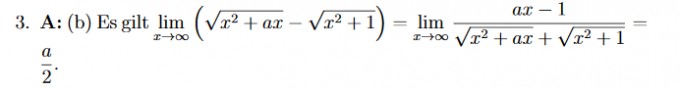

Ich dachte mir, ich ziehe Nenner und Zähler auseinander, also $$\lim\limits_{x\to\infty}ax-1  $$ und $$\frac{1}{\lim\limits_{x\to\infty}\sqrt{x^2+ax}+\lim\limits_{x\to\infty}\sqrt{x^2+1}}  $$, womit ich beim Zähler ∞ bekomme und beim Nenner dann 0, weil $$ \frac{1}{∞}$$. Wieso kommen wir dann bei der Lösung auf $$ \frac{a}{2}$$?

:)

Answer 1

Hi,

auf den zweiten Schritt wurde mit der dritten binomischen Formel erweitert. Da kannst Du alles weitere dann ablesen ;).

Im Nenner kannst Du, bei der Betrachtung im Unendlichen, das ganze zu √x^2 + √x^2 = x + x = 2x vereinfachen und im Zähler kannst Du die -1 getrost ignorieren. Damit ergibt sich, nach kürze, das a/2.

Alles klar?

Grüße

Comments

Oooh, du meinst also, dass man einfach beim letzten Schritt abgeschätzt hat? Also :

---

Nicht notwendigerweise ein ≤, sondern vielmehr ein ≈.

Man vernachlässigt kleinere Potenzen, da die im Unendlichen kaum noch eine Rolle spielen. So würde man bspw auch die Untersuchung von x^3 + ax über eine Abschätzung von x^3 beantworten können, obwohl ≥ gilt (für a > 0).

---

Und wie mir jetzt alles klar ist! :D Vielen lieben Dank!! :)

Answer 2

der Term wurde im Zähler und Nenner mit

√(x^2+ax) +√(x^2+1)  multipliziert . Dann kommst Du auf den angegebenen Term.