Analysis. Gerade soll f(x)= 1/18*x3-1/2*x2+6 in zwei Punkten schneiden

Question

Gegeben ist die Funktion f(x)= 1/18*x³-1/2*x²+6 (mit allen reellen Zahlen) und die Gleichung einer Geraden mit y = m*x+6

Bestimmen sie beide Werte für m so, dass die Funktion f(x) und die Gerade sich an exakt zwei Stellen schneiden!

Ist eine ganz neue Aufgabe^^ (hust MatheAbi hust) Ich kam einfach nicht auf die Lösung :(

Answer 1

die Schnittstellen erhält man durch Gleichsetzen der Funktionsterme:

1/18·x³ - 1/2·x² + 6 = m·x + 6

1/18·x³ - 1/2·x² - m·x  = 0  |  • 18

x³ - 9x² - 18mx = 0

x · (x² - 9x - 18m) = 0

x = 0    oder   x² - 9x - 18m = 0

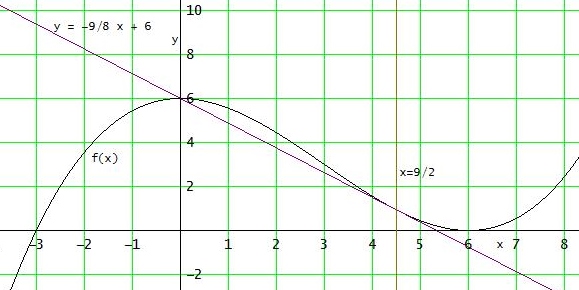
x² - 9x - 18 = 0  $$x^2 + p \cdot x + q = 0$$pq-Formel:  p = - 9 ; q = -18$$x_{1,2} = -\frac { p }{ 2 } \pm \sqrt{ \left(\frac { p }{ 2 }\right)^2-q}$$Da die Lösung  x₁ = 0  bereits feststeht, darf die pq-Formel nur noch eine weitere Lösung ergeben. Das ist der Fall, wenn der Term unter der Wurzel den Wert 0 hat:

(9/2)² + 18m = 0  ⇔   18m = -81/4   ⇔   m = -9/8

Die 2. Lösung ist dann  x₂ = 9/2

Gruß Wolfgang

Comments

Schneidet sich nur einmal

---

jetzt stimmts.

y=-9/8x+6 geht

---

Ich kam eigentlich auf genau dieselbe Lösung, bis auf die Tatsache, das m bei mir = 9/8 und nicht - 9/8 war.... :O

Das Schaubild ergibt jetzt auch Sinn! Ich habe mich mit einem - vertan.....

Dennoch vielen Dank für die ausführliche Lösung!

Answer 2

Meine Skizze könnte da helfen:

Plotlux öffnen

f₁(x) = 1/18·x³-1/2·x²+6f₂(x) = x+6f₃(x) = -x+6f₄(x) = -2x+6f₅(x) = 0x+6Zoom: x(-10…20) y(-20…20)

Eines von diesen m sehe ich bereits. Vielleicht findest du das angeblich vorhandene zweite m .

So ungefähr sehe ich das zweite m hier:

Plotlux öffnen

f₁(x) = 1/18·x³-1/2·x²+6f₂(x) = -1,12x+6f₃(x) = -x+6f₄(x) = -2x+6f₅(x) = 0x+6Zoom: x(-10…20) y(-20…20)

1/18*x³-1/2*x²+6 = mx + 6

1/18*x³-1/2*x² - mx = 0 

1/18 * x * (x² - 9x - 18m) = 0

Ein gemeinsamer Punkt ist immer bei x=0. Nämlich P(0| 6) .

Nun hat (x² - 9x - 18m) entweder eine Nullstelle x=0 oder eine doppelte Nullstelle.

1. Fall Nullstelle x=0 , wenn m=0: (x² - 9x - 0) = x(x-9) .

2. Fall eine doppelte Nullstelle. (x² - 9x - 18m) muss (x - xo)² sein.

(x-xo)² = (x² - 9x + (9/2)²)

(9/2)² = -18m

9²/4 = -18m

-9/8 = m

m = -1.125

Comments

Auf m = 0 kam ich auch, jedoch berührt die Gerade dann das Schaubild nur und schneidet sie nicht, oder? Somit würde sie nur einmal scheniden...

---

Richtig. Der Begriff "schneiden" wird unterschiedlich verwendet / definiert. In der Schule oft einfach als "die Graphen enthalten den gleichen Punkt". D.h. Graphen "schneiden" sich in allen gemeinsamen Punkten.

---

@Mathefreak

Es gibt keine Gerade, die mit dem Graph von f genau 2 Punkte gemeinsam hat,  ohne dass einer davon ein Berührpunkt ist.

---

@Mathefreak: Denke einfach an Schnittmenge. Diese Art von "schneiden" ist hier gemeint und nicht das Durchdringen. Es gibt keine Gerade die das macht, was du interpretiert hattest.

Answer 3

   Vieta das geschmähte Stiefkind;  ich polemisiere hier gegen die ( kontra-intuitive )  Mitternachtsformel.   Eure Lehrer sind nämlich daran schuld, dass euch nix Besseres einfällt.  Die quadratische Gleichung in Normalform

      x  ²  -  p  x  +  q  =  0      (  1a  )

    p  =  x1  +  x2  =  9        (  1b  )

    q  =  x1  x2  =  -  18  m     (  1c  )

    Wie du siehst, habe ich die Vieta Aussagen gleich vermerkt:  gefordert war aber 

        x1  =  x2  =:  x0      (  2a  )

     ( nur eine Nullstelle )  Das setztr du so ein in ( 1b ) und erhältst x0 = 9/2  .   Dann m aus ( 1c )

     q  =  x0  ²  =  81/4  =  -  18  m    |  :  ggt = 9      (  2b  )

   2  m  =  (  -  9/4  )  ===>  m  =  (  -  9/8  )   (  2c  )