Mit Potenzreihenansatz unendlich oft differenzierbar Funktion finden?

Question

Kann mir jemand bei der folgenden Aufgabe helfen? Wäre unendlich dankbar.

Finden Sie mit Hilfe des Potenzreihenansatzes $f(x) = \sum_{k=0}^{\infty}{ c_k x^k}$ eine unendlich oft differenzierbare Funktion $f: (-1,1) → ℝ$ mit

$$(1-x^2) f''(x)-2xf'(x) + 2f(x) = 0 \text{ für } |x| < 1$$

und

$$f(0) = 1 = f'(0)$$

- - -

Answer 1

Nimm doch den Ansatz und leite ihn zweimal ab

$$\begin{aligned}f(x) &= \sum_{k=0}^{\infty} c_k x^k \\ f'(x) &= \sum_{k=1}^{\infty} k c_k x^{k-1} \\ f''(x) &= \sum_{k=2}^{\infty} k(k-1) c_k x^{k-2} \end{aligned}$$

dann setzte die Funktionen in die DGL ein

$$(1-x^2) f''(x) - 2xf'(x) + 2f(x) = 0$$ $$(1-x^2) \left( \sum_{k=2}^{\infty} k(k-1) c_k x^{k-2} \right) - 2x \left( \sum_{k=1}^{\infty} k c_k x^{k-1}\right) + 2\sum_{k=0}^{\infty} c_k x^k = 0$$ das Ganze wird jetzt so sortiert, dass die Koeffizienten vor gleich großen Exponenten von $x$ zusammen gefasst werden: $$\left( \sum_{k=2}^{\infty} k(k-1) c_k x^{k-2} \right) - \left( \sum_{k=2}^{\infty} k(k-1) c_k x^{k} \right) - 2 \left( \sum_{k=1}^{\infty} k c_k x^{k} - \sum_{k=1}^{\infty} c_k x^k\right) + 2c_0= 0$$ $$\left( \sum_{k=0}^{\infty} (k+2)(k+1) c_{k+2} x^{k} \right) - \left( \sum_{k=2}^{\infty} k(k-1) c_k x^{k} \right) - 2 \left( \sum_{k=2}^{\infty} (k-1) c_k x^{k}\right) + 2c_0= 0$$ $$2c_2 + 6c_3 x + \left( \sum_{k=2}^{\infty} (k+2)(k+1) c_{k+2} x^{k} \right) - \left( \sum_{k=2}^{\infty} (k+2)(k-1) c_k x^{k} \right)+ 2c_0= 0$$ $$2(c_0 + c_2) + 6c_3 x + \sum_{k=2}^{\infty} (k+2)\left[ (k+1)c_{k+2} - (k-1) c_k\right] x^{k} = 0$$ damit obige Gleichung erfüllt ist, muss jeder Koeffizient =0 sein. Weiter ist als Anfangsbedingung $f(0)=f'(0)=1$ gegeben. Daraus folgt, dass $c_0=1$ und $c_1=1$ ist. Die weiteren $c_k$ sind dann: $$\begin{aligned} \Rightarrow c_2 &= -c_0 = -1 \\ c_3 &= 0 \\ c_{k+2} &= \frac{k-1}{k+1} c_k\end{aligned}$$ d.h. alle $c_k$ mit geradem $k$ sind ungleich 0 ohne Beschränkung. Also ist die Funktion beliebig oft differenzierbar. (nein deshalb nicht s.Kommentar unten)

Nachtrag: Das Polynom lautet demnach:

$$f(x)= 1 + x -\sum_{n=1}^{\infty} \frac{1}{2n-1}x^{2n}$$

Ich habe die Differenzialgleichung nochmal bei Wolfram Alpha eingegeben und als Lösung hat er mir eine Legendre's Gleichung ausgespuckt

$$f(x)= 1 + x + \frac12 x \big( \ln(1 - x) - \ln(1 + x) \big)$$

Zusätzlich habe ich einen nummerischen Algorithmus (nach Runge Kutta) auf die DGL angesetzt und alle drei Funktionen sehen als Graph so aus:

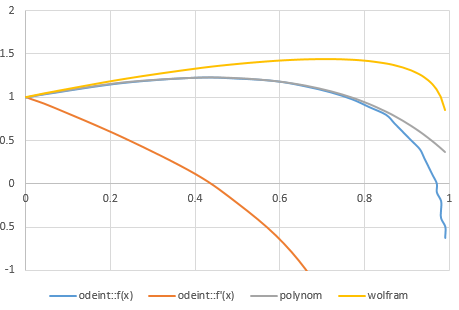
Die nummerische Lösung (f(x) blau; f'(x) orange) und das Polynom (grau; bis 8.Grades) stimmen sehr gut überein. In der Nähe von 1 werden sie aus naheliegenden Gründen 'unscharf'. Warum aber die Lösung von Wolfram Alpha (gelb) so daneben liegt, dafür habe ich keine Erklärung :-/

Gruß Werner

Comments

Pluspunkt für die Rechnung. Kannst du mir den Schluss noch erklären?

Wäre denn z.B. y = x² - 2x nicht unendlich oft differenzierbar?

---

Wäre denn z.B. y = x2 - 2x nicht unendlich oft differenzierbar?

Ja - natürlich. Genau wie $y(x)=0$. Ich hatte das mit dem 'unendlich oft differenzierbar' erst  missverstanden.

Jetzt weiß ich aber nicht, wie man 'unendlich oft differenzierbar' bei einem Polynom unendlichen Grades zeigen kann. Wahrscheinlich muss man zeigen, dass das Polynom für ein $x \in ]-1;1[$ gegen einen endlichen Grenzwert geht. Das sollte aber der Fall sein.

---

Nachtrag bei der Antwort hinzugefügt (s.o.).

Ich würde mich freuen, wenn sich Sandra zum Thema noch mal äußern würde ...

---

Wie hast du die Rekursionsgleichung  für die c_n gelöst? Das ist ja der spannendste Teil der Aufgabe :).

---

Wie hast du die Rekursionsgleichung  für die c_n gelöst?

Damit folgenden Gleichung (s.o. in der Antwort) für alle $x, \, x \in ]-1;+1[$ korrekt ist, müsssen alle Koeffizienten =0 sein: $$2(\underbrace{c_0 + c_2)}_{=0} + 6\underbrace{c_3}_{=0} x + \sum_{k=2}^{\infty} (k+2)\left[ \underbrace{(k+1)c_{k+2} - (k-1) c_k }_{=0} \right] x^{k} = 0$$

Also ist $$\begin{aligned} c_0 + c_2 &= 0 \quad \Rightarrow c_2=-c_0=-1 \\ c_3&=0 \end{aligned}$$ und $$(k+1)c_{k+2} - (k-1) c_k = 0 \quad \Rightarrow c_{k+2}=\frac{k-1}{k+1}c_{k}$$ Dann ist: $$\begin{aligned} c_2 &= -1 = -\frac11 \\ c_4& =\frac{2-1}{2+1} \left(-\frac11 \right)=-\frac13 \\ c_6&=\frac{4-1}{4+1} \left( -\frac13\right) = -\frac15 \\ c_8 &= \frac{6-1}{6+1} \left( -\frac15 \right) = -\frac17 \\ & \text{usw.}\end{aligned}$$

und alle $c_k$ mit ungeradem $k>1$ sind =0, da $c_3=0$ ist (s.o.).

---

Achso, also hast du die ersten Glieder per Hand berechnet und dann die Lösung gesehen. Unter "berechnet" habe ich gedacht, dass man aus c_(k+2)=(k-1)/(k+1) c_k

und c_2 = -1

direkt herleiten kann, dass

c_2k =-1/(2k-1)

Aber wenn man letzteres schon weiß, dann kann man ja Induktion bemühen.

---

... direkt herleiten kann, dass c_2k =-1/(2k-1)

Ja sicher, ist aber doch trivial: $$c_{2k} = \frac{-1}{2k-1}$$ ist korrekt für $k=1$ und Übergang von $k$ nach $k+1$ gibt

$$\begin{aligned}c_{2k+2} &= \frac{2k-1}{2k+1} c_{2k} = \frac{2k-1}{2k+1} \cdot \frac{-1}{2k-1} \\ \space &= \frac{-1}{2k+1} =\frac{-1}{2(k+1)-1} \end{aligned}$$ q.e.d.