Also Klara, hier ist eine Abbildung des Kreissektors (Kreisauschnitts):
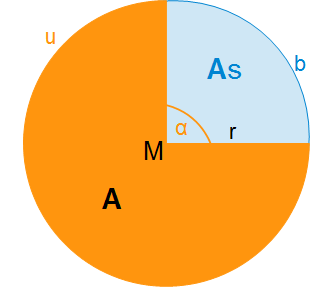
Den Winkel α nennt man auch Zentriwinkel oder Mittelpunktswinkel. Die Länge "b" nennt man Länge des Kreisbogens. Du hast in der Aufgabe d), den Flächeninhalt und den Zentriwinkel gegeben. Es gibt nun folgende Formeln:$$A=r^2\cdot \pi \cdot \frac{\alpha}{360}$$ Und wenn du die Länge des Kreisbogens schon kennst:$$A=\frac{1}{2}\cdot b\cdot r$$ Wir kennen aber nur den Flächeninhalt un den Zentriwinkel, d.h. wir müssen eine Formel nach der gesuchten Variable umstellen. Da du den Radius suchst, so:$$A=r^2\cdot \pi \cdot \frac{\alpha}{360} \quad |:\pi \cdot \frac{\alpha}{360}$$$$\frac{A}{\pi \cdot \frac{\alpha}{360}}=r^2 \quad |\sqrt{}$$$$r=\sqrt{\frac{A}{\pi \cdot \frac{\alpha}{360}}}$$ Jetzt musst du nur noch die Angaben einsetzen:$$r=\sqrt{\frac{76.8}{\pi \cdot \frac{108}{360}}}≈ 9.027m$$ Bei manchen Aufgaben musst du auch die Länge des zugehörigen Kreisbogens berechnen, dafür gibt es folgende Formel:$$b=2\cdot r \cdot \pi \cdot \frac{\alpha}{360}$$ Diese Formel kannst du natürlich auch nach "r" umstellen, brauchst du dabei Hilfe?
Volia!
