Vom Duplikat:
Titel: Wahrscheinlichkeitsrechnung
Stichworte: wahrscheinlichkeit,wahrscheinlichkeitsrechnung,population,stochastik
In der Vorlesung haben wir die hypergeometrische
Verteilung kennengelernt. Mit der dort verwendeten Notation wird diese
beschrieben durch
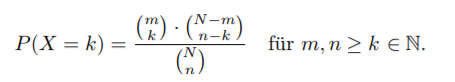
In diesem Zusammenhang betrachten wir nun Ruckfangmethoden. Diese werden an-
gewendet, um die Größe N einer Population zu schätzen. Im einfachsten Fall werden
aus dieser Population M Individuen eingefangen, markiert und wieder freigelassen.
Nachdem sich die markierten Individuen mit der ubrigen Population vermischt ha- ¨
ben, wird eine zweite Stichprobe von n Individuen entnommen und festgestellt, wie
groß die Anzahl m der darunter befindlichen markierten Individuen ist. Man sch¨atzt
nun die Größe N der Population indem man davon ausgeht, dass der Anteil der
markierten Individuen in der zweiten Stichprobe etwa dem Anteil aller markierten
Individuen an der der Gesamtpopulation entspricht, also dass 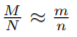 gilt.
gilt.
Nehmen Sie nun an, dass die Population aus 500 Individuen bestehe, von denen
100 markiert seien. Bei Ihrer zweiten Stichprobe fangen Sie 20 Individuen ein.
(b) Wie groß ist die Wahrscheinlichkeit, dass Sie bei der zweiten Stichprobe
dann tatsächlich genau 4 markierte Individuen fangen (und Ihre Schätzung
für N dementsprechend exakt ist)?
(c) Wie groß ist die Wahrscheinlichkeit, dass Sie bei der zweiten Stichprobe 3, 4
oder 5 (mindestens drei und höchstens fünf) markierte Individuen fangen.
Mein Ansatz:
b) 100/500 = 1/5
20 * 1/5 = 4
Ist die Wahrscheinlichkeit dementsprechend bei 100%, dass ich bei 20 Individuen 4 markierte finde? Inwiefern zeigt mir das, dass meine Schätzung nun für N exakt ist?
c) Dafür habe ich noch keinen Ansatz, wahrscheinlich ergibt sich das aus Aufgabe b), allerdings zweifel ich daran, das Aufgabe b richtig ist...