Hallo Srh97,
Du hast die Gerade in vektorieller Form gegeben. Ich unterstelle daher, dass Ihr schon die Normalenform einer Geraden durch genommen habt. Bei der Hesseschen Normalform einer Geraden $$\vec{n} \cdot \vec{x} = d$$ ist \(d\) der Abstand zum Ursprung. Voraussetzung ist, dass \(|\vec{n}|=1\) ist. Da \(\vec{n}\) senkrecht auf der Geraden steht, ist der gegebene Richtungsvektor der Geraden \(\vec{r}= \begin{pmatrix}-1 & 1\end{pmatrix}^T\) auch ein Normalenvektor der gesuchten Tangente, die lt. Aufgabenstellung senkrecht auf der Geraden stehen soll. Für die Hessesche Normalform müssen wir ihn nur noch normieren, d.h. auf eine Länge von 1 bringen. Es ist: $$\vec{n} = \frac{1}{|\vec{r}|} \cdot \vec{r} = \frac{1}{\sqrt{(-1)^2+1^2}} \cdot \begin{pmatrix}-1 \\ 1\end{pmatrix} = \frac{\sqrt{2}}{2}\begin{pmatrix}-1 \\ 1\end{pmatrix}$$ Da der Mittelpunkt des Kreises im Ursprung liegt, ist der Abstand aller Tangenten des Kreise vom Ursprung \(=R=\sqrt{50} = 5\sqrt{2}\). Das brauche wir nur noch einsetzen und die Tangenten sind gefunden:
$$\vec{n} \cdot \vec{x} = d \quad \Rightarrow \frac{\sqrt{2}}{2}\begin{pmatrix}-1 \\ 1\end{pmatrix} \cdot \vec{x} = \pm5\sqrt{2}$$ plus/minus weil die Tangente auf beiden Seiten des Kreises senkrecht auf der Gerade steht und den gleichen Abstand hat. Multiplikation obiger Gleichung mit \(\sqrt{2}\) bringt sie noch in eine gefälligere Form:
$$\begin{pmatrix}-1 \\ 1\end{pmatrix} \cdot \vec{x} = \pm10 \quad \text{bzw: } -x + y = \pm10; \quad y = x \pm 10$$ Das ganze noch mal graphisch:
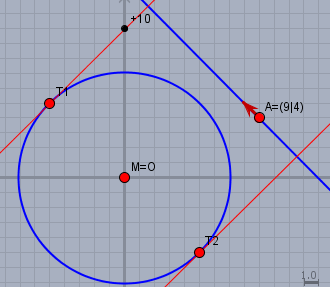
Falls ihr die Hessesche Normalform noch nicht gehabt hat, und Du eine Lösung mit linearen Funktionen benötigst, so frage bitte noch mal nach.
Gruß Werner