Ok, dann hier mal ein möglicher Weg mit dem TI-Nspire CX:
(1) Drücke auf Home und füge die Applikation "Lists & Spreadsheet" zum aktuellen Dokument hinzu. Im einfachsten Falle ist das die erste Seite eines neuen Dokuments.
(2) Schreibe in die Formelzelle (in der =-Zeile) der Spalte A das Kommando
=seq(a,a,0,100,1)
um die Spalte A mit den Zahlen 0, 1, 2, 3 ,... 99, 100 zu füllen. Gib der Spalte A den Namen x indem du in ihre Kopfzelle (in der Label-Zeile) x hinenschreibst. Die Vergabe von Spaltennamen ist wichtig für den zugriff auf die Spalten von anderer Stelle aus.
(3) Schreibe in die Formelzelle der Spalte B das Kommando
=binompdf(100,1/6,'x)
um die Spalte B mit den entsprechenden Wahrscheinlichkeiten P(X=x) der hier zu untersuchenden Binomialverteilung zu füllen. Beachte das Apostroph vor dem x! Nenne die Spalte B zum Beispiel d.
(4) Die Tabelle enthält nun die gesuchte Wahrscheinlichkeitsverteilung. Man kann die Spalten in der Breite anpassen und in der Tabelle herumscrollen. Das Ergebnis könnte etwa so aussehen:
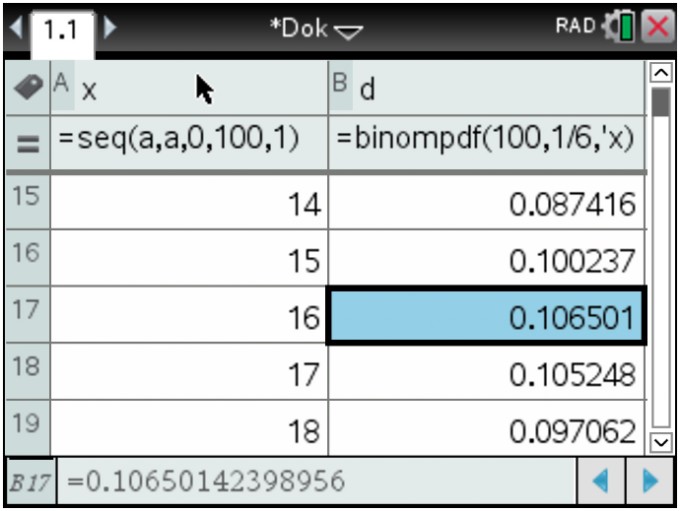
Markiert habe ich mal die Zelle B17 mit der Wahrscheinlichkeit P(X=16) für das Auftreten von genau 16 Sechsen.
(5) Nun soll die Verteilung graphisch dargestellt werden. Wähle dazu
menu - 3: Daten - 8: Ergebnisdiagramm
und darin die Einstellungen
X-Liste: x
Ergebnisliste: d
Anzeige ein: Neue Seite
so wie hier:
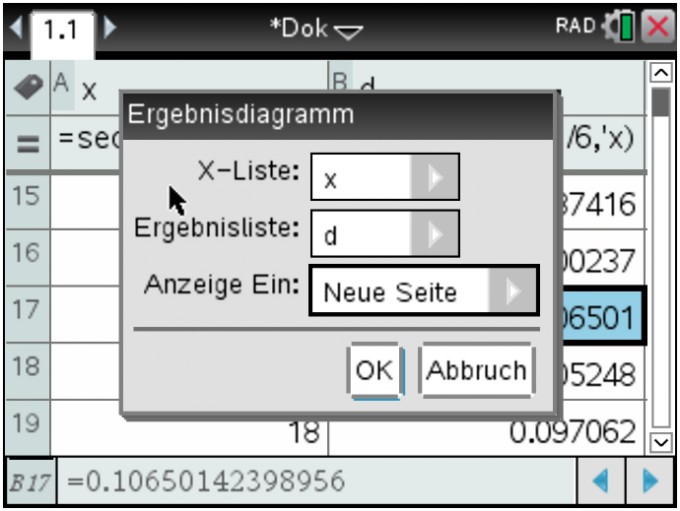
Im Ergebnis zeigt die neue Seite ein noch etwas unbefriedigend skaliertes Histogramm der zu untersuchenden Verteilung:
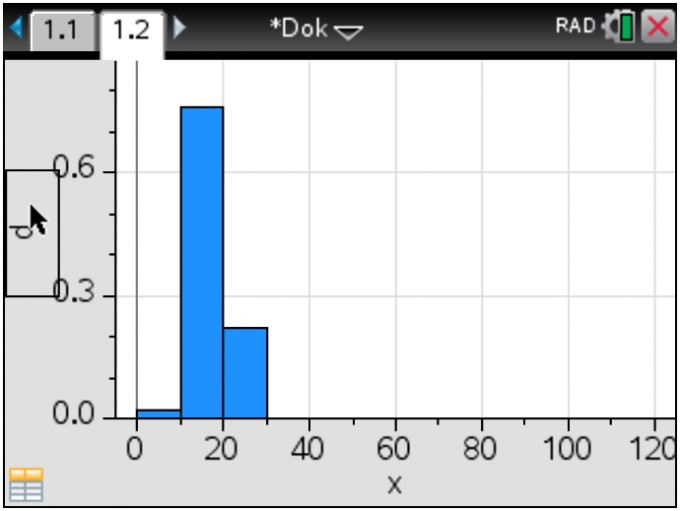
Offenbar liegt fast die gesamte Wahrscheinlichkeit zwischen 0 und 30, so dass eine Beschränkung auf der x-Achse sinnvoll erscheint.Auch die Breite der Flächen kan angepasst werden.
(6) Wähle dazu über menu oder Dokumentwerkzeuge
2: Histogramm-Eigenschaften - 2: Säuleneinstellungen - 1: Gleiche Säulenbreite
und darin die Einstellungen
Breite 1 und Ausrichtung 10.5
Die Einstellung zur Ausrichtung bewirkt das Zentrieren der Säulen über den Ticks der x-Achse. Die 10 vor dem Punkt ist dabei unwichtig, die 5 danach ist entscheidend.
(7) Wähle nun über menu oder Dokumentwerkzeuge
5: Fenster/Zoom - 1: Fenstereinstellungen
passend erscheinende Werte, etwa diese:
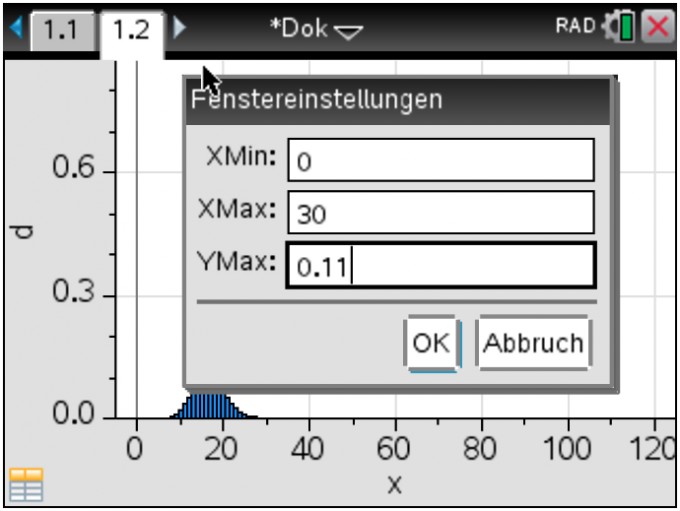
(8) Füge bei Bedarf noch etwas Text hinzu und speichere das ganze Dokument zwecks späterer Verwendung als Vorlage ab. Die zweite Seite sollte jetzt so aussehen:
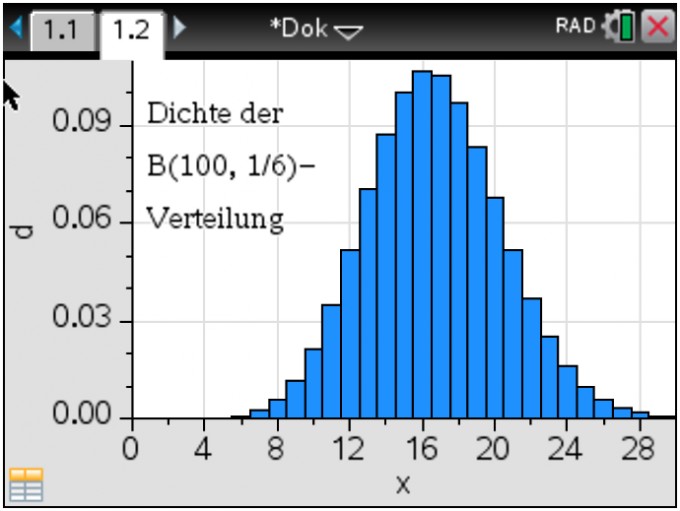
(9) Die Anleitungen zu diesem GTR geben leider oft nicht die notwendigen Detais, die hier benötigt werden, daher meine etwas ausführliche Darstellung.