Kardinalität von Vereinigungen mit Induktion zeigen

Question

Die Aufgabe ist es diese Gleichung zu zeigen;

$$\# \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) = \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right)$$

Ich habe die Induktion gemacht, aber bei dem letzten Induktionsschritt komme ich nicht weiter

(P ist die Potenzmenge)

Hier ein Bsp:

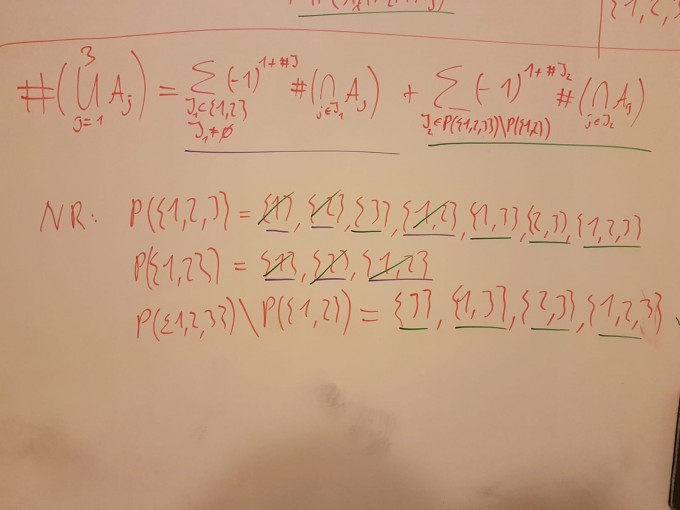
Der Induktionsschritt (n →n+1):

$$\# \left( \bigcup _ { j = 1 } ^ { n +1 } A _ { j } \right) = \sum _ { J \subset \{ 1 , \ldots , n+1 \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right)$$

$$\# \left( \bigcup _ { j = 1 } ^ { n+1 } A _ { j } \right) = \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right) + \sum _ { J\prime \in P \{ 1 , \ldots , n+1 \} \backslash P \{ 1 , \ldots , n \} }  ( - 1 ) ^ { 1 + \# J\prime } \; \# \left( \bigcap _ { j \in J\prime } A _ { j } \right) $$

$$\# \left( \bigcup _ { j = 1 } ^ { n+1 } A _ { j } \right) \overset{\text{I.V.}}{\underset{\text{}}{=}} \# \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right)  + \sum _ { J\prime \in P \{ 1 , \ldots , n+1 \} \backslash P \{ 1 , \ldots , n \} }  ( - 1 ) ^ { 1 + \# J\prime } \; \# \left( \bigcap _ { j \in J\prime } A _ { j } \right) $$

$$\# \left( \bigcup _ { j = 1 } ^ { n+1 } A _ { j } \right) = \# \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) + \# \left( A _ { n + 1 } \backslash \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) \right)$$

Hat einer einen Vorschlag wie ich von der vorletzten Zeile in die letzten Zeile komme? bzw. wie das konkret aufschreibe ?

Comments

Dein Induktionsschritt ist unverstaendlich und aller Wahrscheinlichkeit nach falsch. Was willst Du denn an der Stelle, wo Du angeblich die Induktionsvoraussetzung benutzt, gemacht haben?

---

Ich kann nachvollziehen dass es bisschen unverständlich ist. Ich habe in dem Schritt davor alle Teilmengen raus genommen in denen n+1 ein Element war damit ich die Induktionsvoraussetzung anwenden kann. P({1,...,n+1})\P({1,...,n}) sind alle Teilmengen in denen n+1 vorkommt. Siehe dazu das Beispiel.

---

Wenn Du das anstaendig aufschreiben willst, dann so, dass man auch was erkennen kann. Der Induktionsschritt beginnt immer damit, dass man eine Seite der Aussage für \(n+1\) so umformt, dass die Induktionsvoraussetzung eingebracht werden kann. Dazu gibt es hier zwei Moeglichkeiten. Bei der ersten fasst man die letzten beiden der \(n+1\) Mengen zusammen. $$\#(A_1\cup\ldots\cup A_n\cup A_{n+1})=\#(A_1\cup\ldots\cup(A_n\cup A_{n+1}))$$ Dann steht da eine Vereinigung von \(n\) Mengen und man kann die Induktionsvoraussetzung inverstieren. Die zweite Moeglichkeit ist, die ersten \(n\) Mengen zusammenzufassen. $$\#(A_1\cup\ldots\cup A_n\cup A_{n+1})=\#((A_1\cup\ldots\cup A_n)\cup A_{n+1})$$ Dann kann man \(\#(A\cup B)=\#A+\#B-\#(A\cap B)\) benutzen und die Induktionsvoraussetzung im naechsten Schritt investieren (sogar zwei Mal).

So und nicht anders faengt jeder vernuenftig aufgeschriebene Induktionsschritt an.

---

I.V. :

$$\# \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) = \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right)$$

I.S. :

$$\# \left( \bigcup _ { j = 1 } ^ { n+1 } A _ { j } \right) = \# \left( A _ { 1 } \cup \ldots \cup A _ { n } \cup A _ { n + 1 } \right) = \# \left( \left( A _ { 1 } \cup \ldots \cup A _ { n } \right) \cup A _ { n + 1 } \right)$$

$$ = \# \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) + \# A _ { n+1 } - \# \left( \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) \cap A _ { n + 1 } \right)$$

$$ \overset{\text{I.V.}}{\underset{\text{}}{=}} \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right) + \# A _ { n+1 } \\- \# \left( \left(  \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right) \right) \cap A _ { n + 1 } \right)$$

So ? Und jetzt ?

---

Sorry die letzte Zeile ist falsch

$$ \overset{\text{I.V.}}{\underset{\text{}}{=}} \sum _ { J \subset \{ 1 , \ldots , n \} } ( - 1 ) ^ { 1 + \# J } \; \# \left( \bigcap _ { j \in J } A _ { j } \right) + \# A _ { n+1 } \\- \# \left( \left( \bigcup _ { j = 1 } ^ { n } A _ { j } \right) \cap A _ { n + 1 } \right) $$

---

Zweite Formelzeile: Wenn Du schon mit dem grossen Vereinigungszeichen arbeitest, solltest Du aus Konsistenzgruenden auch dabei bleiben. Du schreibst also \(\bigcup_1^{n+1}A_j=\left(\bigcup_1^nA_j\right)\cup A_{n+1}\).

Dritte Formelzeile, dritter Ausdruck: Da kann man das Distributivgesetz verwenden und hat wieder eine Vereinigung von \(n\) Mengen. Da kommt dann zum zweiten Mal die Induktionsvoraussetzung ins Spiel.

[Der Kommentar ist zu Deinem vorletzten]