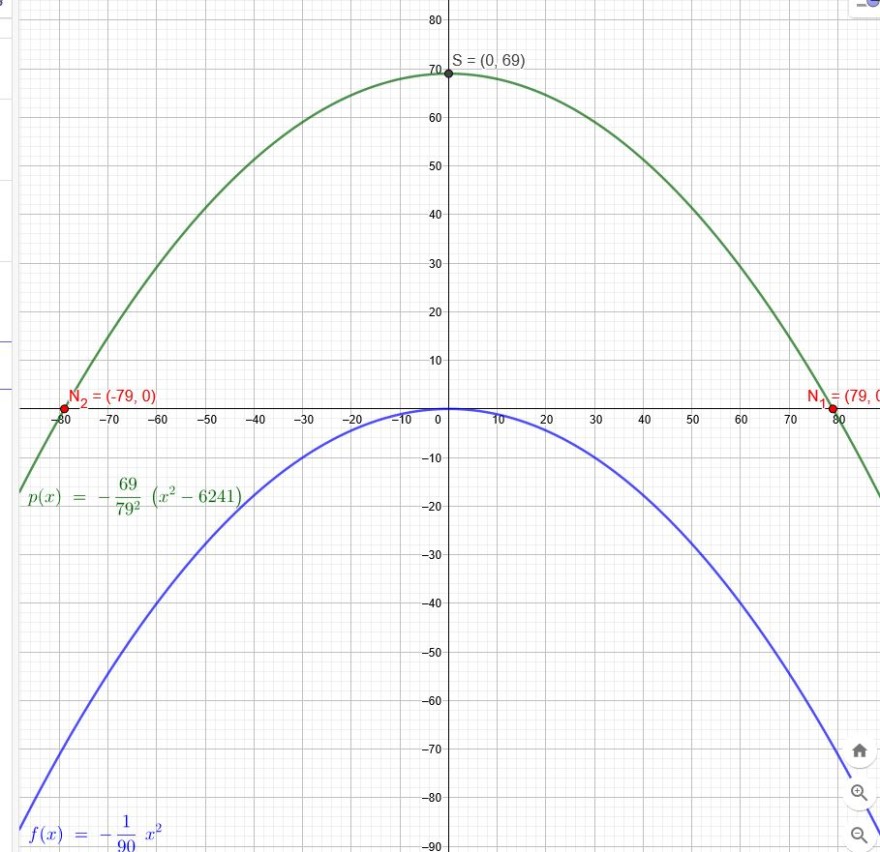
Der Bogen der Müngstener Brücke lässt sich durch eine Parabel mit der Gleichung \(f(x):= -\frac{1}{90} x^2\) beschreiben Die Spannweite beträgt 158 m die Bogenhöhe 69m. Passen diese Daten zusammen?
Die Spannweite beträgt 158 m:→\(N_1(79|0)\) oder \(N_2(-79|0)\)
\(p(x)=a(x-79)(x+79)=a(x^2-79^2)\)
Bogenhöhe 69m :→\(S(0|69)\)
\(p(0)=a(0-79^2)=-79^2a\)
\(-79^2a=69\) \(a=-\frac{69}{79^2}\)
\(p(x)=-\frac{69}{79^2}(x^2-79^2)=-\frac{69}{79^2}x^2+69\)
\(p(x)≠f(x)\)