mache Dir eine Skizze des Rechtecks, so wie diese:
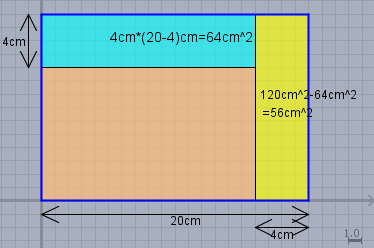
Das blau umrandete Rechteck ist das Ausgangsrechteck. Von dem weiß man, dass es 20cm lang ist. Nun schneidet man zunächst 4cm links ab (das gelbe Rechteck) und dann 4cm oben (das blaue Rechteck). Das obige blaue Rechteck ist 4cm breit und \((20-4)\text{cm} = 16\text{cm}\) lang. Es hat folglich eine Fläche von $$F_{\text{blau}} = 4 \text{cm} \cdot 16 \text{cm} = 64 \text{cm}^2$$ Die Verkleinerung des Flächeninhalts soll 120cm2 betragen. Die Verkleinerung ist die Summe aus dem blauen und dem gelben Rechteck. Also hat die gelbe Fläche einen Flächeninhalt von $$F_{\text{gelb}} = 120 \text{cm}^2 - F_{\text{blau}} = 120 \text{cm}^2 - 64 \text{cm}^2 = 56 \text{cm}^2$$ und da das blaue Rechteck auch 4cm breit ist, bleibt für seine zweite Seite $$\cdots = \frac{F_{\text{gelb}}}{4 \text{cm}} = \frac{56 \text{cm}^2}{4 \text{cm}} = 14 \text{cm}$$ und diese ist identisch mit der gesuchten Breite des Ausgangsrechteck.
Gruß Werner