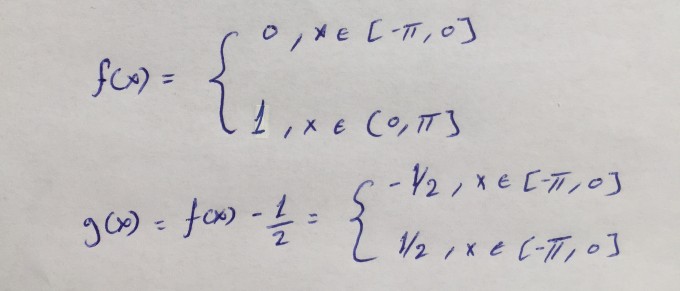 Hi !
Hi !
Gegeben sind folgende Funktionen und ich muss die Fourierreihe Sg(x) berechnen mein Problem ist aber , dass man bei Teilaufgabe i) bestimmen muss ob die Funktion g(x) gerade oder ungerade ist ich glaube damit man sagen kann ob an bzw. bn = 0 ist.
Habe gegoogelt und stand irgendwas mit -f(x)=f(-x) aber ich weiß nicht wie das zu meiner Funktion passt , da ich nur Zahlen habe :/
Laut Musterlösung ist die funktion g(x) ungerade abet ich weiß nicht wie man drauf gekommen ist :|