Lösen von 1/2+1/2 sin(pi/15*t)=0,95 durch Substitution

Question

Aufgabe:

1/2+1/2 sin*(pi/15*t)=0,95

... sin(pi/15*t)=0,9

Danach komme ich nicht weiter

Problem/Ansatz:

Wäre jemand so lieb und könnte mir verständlich die Aufgabe vorrechnen?

Comments

Vom Duplikat:

Titel: Berechnen Sie die Lösungen dieser Gleichung A(t)=0,95

Stichworte: analysis

Aufgabe:

Mit A(t)=1/2+1/2*sin(pi/15*t)

Kann mir das jemand einfach vorrechnen, ich bin leider nicht die hellste was Mathe angeht...

---

Fehler, gleich neu! :-)

---

Und jetzt noch k * 2π dazuaddieren

Ich denke, man muss die Periode des Sinusterms  [2π / (π/15))dazuaddieren].

---

Es hat sich eh ein Fehler eingeschlichen.

---

Das ist doch die selbe Aufgabe wie vorhin, oder nicht?

---

Hast recht, ich habe die Fragen zusammengeführt.

---

Vielen Dank !

---

Nochmal als Anmerkung

Mein Satz vom direkten Auflösen besagt:

Jede Gleichung in der die aufzulösende Unbekannte immer nur an genau einer Stelle auftritt, kann immer direkt zur Unbekannten aufgelöst werden.

Eine Substitution ist nicht erforderlich, könnte aber gemacht werden um die Gleichung etwas überschaubarer zu machen.

1/2 + 1/2·SIN(pi/15·t) = 0.95

1/2·SIN(pi/15·t) = 0.95 - 1/2

SIN(pi/15·t) = (0.95 - 1/2)/(1/2)

pi/15·t = ARCSIN((0.95 - 1/2)/(1/2)) + k·2·pi oder pi - ARCSIN((0.95 - 1/2)/(1/2)) + k·2·pi

t = (ARCSIN((0.95 - 1/2)/(1/2)) + k·2·pi)/(pi/15)

Ich habe jetzt nur den ersten Lösungszweig betrachtet. Der andere wird aber genauso behandelt.

---

@Mathecoach Dankeschön! Wieso verläuft aber die sin(z) achseymmetrisch zu x=pi/2 bzw.woran kann man es erkennen?

---

Du solltest die Sinus-Funktion skizzieren können.

Die Sinus-Funktion ist Achsensymmetrisch zu senkrechten durch die Extrempunkte und punktsymmetrisch zu ihren Wendepunkten.

Das siehst du auch am Graphen und man kann es auch mathematisch nachweisen. Da ein mathematischer Nachweis aber nichts fürs Verständnis bringt begnüge ich mich hier mal mit der Skizze:

Answer 1

sooo macht man das:$$\frac{1}{2}-\frac{1}{2}\sin\left(\frac{\pi}{15}\cdot t\right)=0.95 \quad |-\frac{1}{2} \quad |:\frac{1}{2}$$$$\sin\left(\frac{\pi}{15}\cdot t\right)=0.9$$ Substituiere nun \(u:=\frac{\pi}{15}\cdot t\) und erhalte:$$\sin\left(u\right)=0.9$$$$u=\arcsin(0.9)+2k\pi$$$$u'=\pi-\arcsin(0.9)+2k\pi$$ Und nun einfach rücksubstituieren:$$\frac{\pi}{15}\cdot t_{1}=\arcsin(0.9)+2k\pi \quad |:\frac{\pi}{15}$$$$t_{1}=\frac{15\arcsin(0.9)}{\pi}+30k$$ Und:$$t_{2}=\frac{15(\pi-\arcsin(0.9))}{\pi}+30k$$

Comments

Du solltest die 1/2 subtrahieren und nicht addieren. Die Gleichung besitzt reelle Lösungen.

---

@ Larry: "subtrahieren"

@ racine_carrée: Substitution ist hier eigentlich unsinnig und macht unnötig Arbeit. Der Term ist doch auch so übersichtlich genug.

---

Substitution ist hier eigentlich unsinnig und macht unnötig Arbeit. Der Term ist doch auch so übersichtlich genug.

Das stimmt, allerdings wird auch in meinem Schulbuch diese Methode "empfohlen".

---

@ racine_carrée: Das ist vielleicht der Didaktik geschuldet. Schul- und andere Lehrbücher lassen oft Sachverhalte zum Selbstentdecken offen. Ich habe hier ein Schulbuch liegen, dass in einem speziellen Zusammenhang eine Methode empfiehlt, die ich nie benutzen würde und auch niemandem empfehlen würde. Ein paar Seiten später soll der Schüler im Rahmen einer Übungsaufgabe herausfinden, warum eine andere Methode wesentlich praktischer ist als die zuvor gezeigte... :-)

---

Im Lösung steht z1=1,12 und z2=2,02 ...wie kommt man drauf?

---

Was setzt man in u ein ? Und wieso bildet man noch die Ableitung von u'

Gibt es vielleicht einen einfacheren Lösungsweg...?

---

Rücksubstitution:$$\frac{\pi}{15}\cdot t_{1}=\arcsin(0.9)+2k\pi \quad |:\frac{\pi}{15}$$$$ t_{1}=\frac{15\arcsin(0.9)}{\pi}+30k$$ Und:$$ t_{2}=\frac{15(\pi-\arcsin(0.9))}{\pi}+30k$$

---

Hallo Wurzel,
bei dir steht in der ersten Zeile
1/2 minus 1/2 ....
In der Aufgabenstellung heißt es
1/2 plus 1/2 ....

---

Ja, der Fehler ist behoben.

---

Ja, der Fehler ist behoben.

Vielleicht sollte sich Georg mal ein Beispiel daran nehmen!

---

Ja, der Fehler ist behoben.

Vielleicht sollt sich Georg mal ein Beispiel daran nehmen:

https://www.mathelounge.de/624452/berechnen-sie-die-betragsungleichungen#c624565

Answer 2

Falls ich nicht ganz auf den Kopf gefallen bin

1/2+1/2 sin(pi/15*t) = 0,95
...
sin ( pi/15*t ) = 0,9 | arcsin

Bogenmass
pi / 15 * t = arcsin(0.9)
pi / 15 * t = 1.12
t = 5.35

Probe
1/2+1/2 sin(pi/15*t) = 0,95
sin(pi/15*5.35) = 0,9
sin(1.12) = 0,9
0.9 = 0.9
Da die sin Funktion periodisch ist
gibt es unendlich viele Lösungen.

Comments

Falls ich nicht ganz auf den Kopf gefallen bin
....  t = 5.35
....  Da die sin Funktion periodisch ist
gibt es unendlich viele Lösungen.

Es gibt sogar jeweils zwei verschiedene Lösungen innerhalb jeder Periode, weil die Sinusfunktion innerhalb einer Periode jeweils doppeldeutig ist:

pi / 15 * t = arcsin(0.9)
pi / 15 * t = 1.12   oder  π/15 * t = π - arcsin(0.9)

---

Danke fürs beantworten!!

---

sin ( pi/15*t ) = 0,9
Im Lösungsbuch steht z1=1,12 und z2=2,02 ...wie
kommt man drauf ?

Ich kenne die Originalfragestellung nicht vermute aber
das pi/15*t durch z substituiert werden soll.
z = pi/15*t
sin ( z ) = 0.9
z = arcsin ( 0.9 )
z = 1.12

Der Taschenrechner zeigt nur eine Lösung an.

Der Graph zeigt dir auch die zweite angegebene
Lösung an ( Schnittpunkt zwischen blau und rot ).
z = 2.02

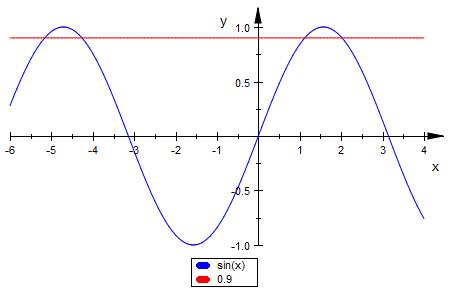
Es gibt aber auch noch unendlich viele weitere.

---

Ich hab's verstanden. Du gibst die ausführlichsten Erklärungen... Vielen Dank dafür!:)

---

Wäre cool wenn man dich für 2Wochen irgendwie für Nachhilfe buchen könnte :D ...

---

Ich kenne mich mit Nachhilfe übers Internet geben
( Skype ? ) nicht aus.
Stell weiterhin Fragen ein. Durch Problemlösung
lernt man eh am meisten.
Ansonsten findest du in meinen Profil meine
e-mail Adresse die du gern nutzen kannst.

---

Cool. !!

---

@georgborn dürfte ich dich kurz nochmal stören... wie schon erwähnt im Buch kommen sie auf 2,02

Durch diese Rechnung: pi/2+(pi/2-1,12)=2,02

Wie kommen die auf diese Rechnung?

---

Bildlich hergeleitet ( siehe oben meine Darstellung
der sin-Funktion )
Die sin-funktion ist achsensymmetrisch zu x = PI/2
oder 90 °.

Nun ist der Abstand zwischen PI/2 ( dem Hoch-
punkt ) und 1.12 ( dem ersten Schnittpunkt ) =
PI/2 minus 1.12 = 0.45
d.h. der Abstand des Schnittpunkts ist 0.45 bis
zur Symmetrieachse.
Auf der andere Seite ist der Wert PI/2 + 0.45
= 2.02 ( 2.02 | 0.9 )
Verknüpft man beide Teilrechnungen ergibt sich
PI/2 + ( PI/2 - 1.212 ) 

---

Vieleeen Dank!

---

Erfreulich, dass georgborn wenigstens bei deiner Nachfrage bzgl. der Lösung mit Substitiution auf die unverzichtbare Angabe der zweiten Lösung innerhalb einer Periode einging.

Ohne diese Nachfrage würde seine völlig unvollständige Antwort jetzt noch - von seiner Seite aus - unkommentiert so dastehen, da er es wieder einmal nicht für notwendig hielt, auf meinen Fehlerhinweis unter seiner Antwort überhaupt einzugehen.

---

... Ich finde gut wie der Herr Georgborn erklärt. :)  könntest du mir kurz erklären wieso verläuft die sin(z) an der Stelle x=pi/2 Achsensymmetrisch woran sieht man es?

---

Sorry, aber georgborn ( = Herr Born :-) ) wird das sicher gern selbst übernehmen. Und ich möchte ungern seinen Zorn erregen :-)

Deshalb beschränke ich mich unter seinen Antworten auf sachliche Fehlerhinweise, die er aber regelmäßig nicht zur Kenntnis nimmt!

---

Wenn du ein Lot vom Hochpunkt zur x-Achse
fällst haben alle Punkte auf der Lotstrecke
die Werte ( x | y ) ( PI/2 | ... ) oder
x = PI/2
Die sin-Funktion ist dazu achsensymmetrisch.
Siehe oben den Graph