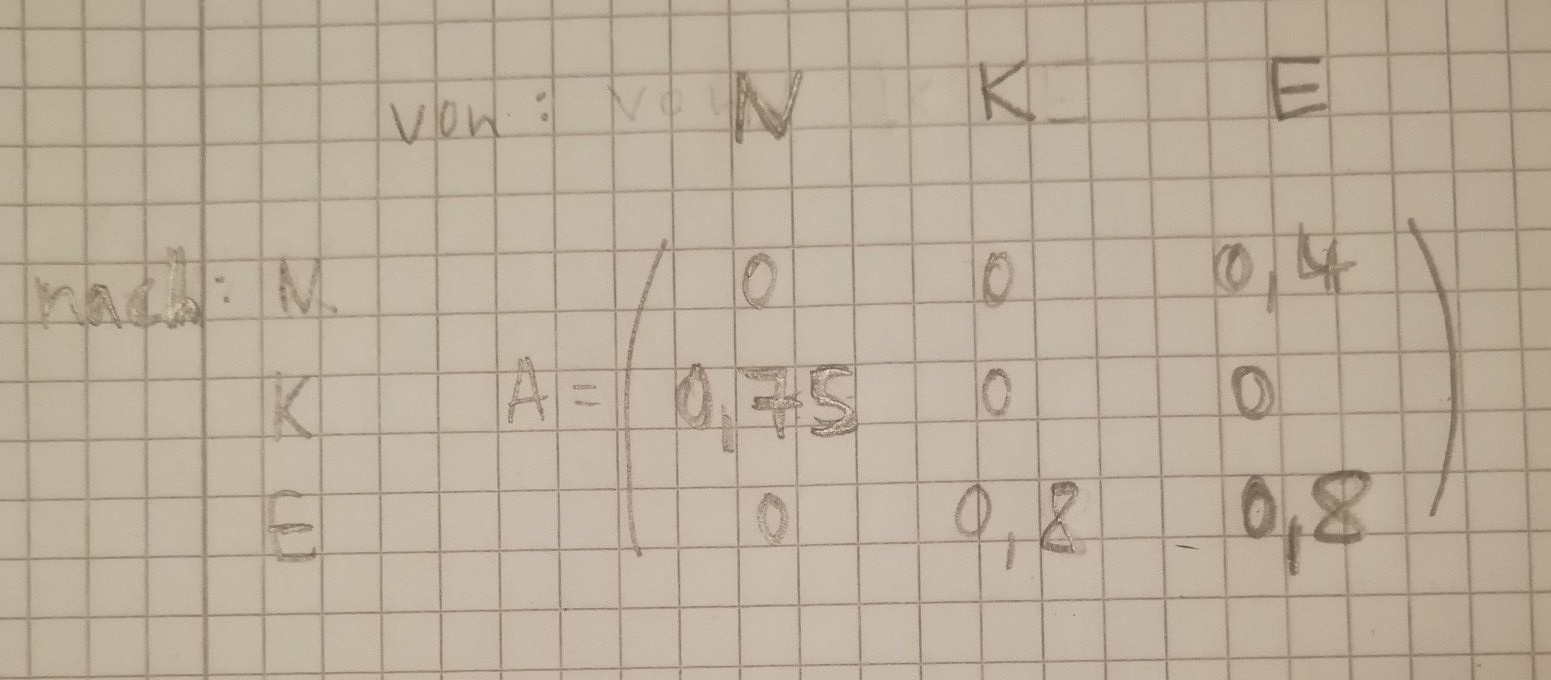Gegeben:
Bei der Aufzucht von Rindern unterscheidet man zwischen Neugeborenen (N), einjährigen Kälbern (K) und geschlechtsreifen erwachsenen Tieren (E), den Kühen und Bullen (mindestens zweijährig). Um eine Rinderherde wirtschaftlich erfolgreich zu betreiben, muss man Kenntnisse über die Anzahl der Geburten, der Todesfälle und der Entnahmen durch Schlachtung oder Verkauf haben. Zudem muss die Verteilung der Herde in den drei Altersstufen (N, K, E) bekannt sein.
In der hier betrachteten Rinderherde werden die Übergänge zwischen den Altersstufen innerhalb eines jahres durch die folgende Matrix A angegeben:
"Siehe Bild"
Aufgabe:
Stellen Sie die Entwicklungen der Rinderherde durch einen Übergangsgraphen dar. [..] Bestimmen Sie [...] den Anteil der Neugeborenen, die das Erwachsenenstadium erreichen.
Die Lösung lautet:
[...] Es erreichen 0,75 · 0,8 = 0,6 = 60 % der Neugeborenen das Erwachsenenstadium.
Problem/Ansatz:
Meine Frage lautet:
Woher weiß ich, dass ein Neugeborenes in einem Jahr zu einem Kalb heranwächst? Wird das vorausgesetzt?
Oder denke ich ganz falsch? Irgendwie blicke ich da gerade nicht ganz durch...
Die Rechnung:
0,75•0,8 ergibt für mich Sinn. 75 Prozent werden überhaupt zum Kalb und von den 75 Prozent wiederum werden 80 Prozent zum erwachsen Rind.
Das heißt schlicht, ich kann aus der Matrix schließen: 1 Jahr zum Kalb und 2 Jahr zum erwachsen Tier ... Ist das so richtig?
Mein Problem kam in einem anderen Forum schon auf, wo die Antwort lautete:
"Auf welchem Weg kann denn ein Neugeborenes zum Erwachsenen werden?
Es muss nach einem Jahr zum Kalb werden und nach einem weiteren Jahr zum erwachsenen Tier.
Gibt es eine andere Möglichkeit?
Nein!
Von allen Neugeborenen werden 75% nach einem Jahr zum Kalb (der Rest ist nicht mehr im System). Von diesen 75% erreichen 80% nach einem weiteren Jahr das Erwachsenenstadium.
Wie berechnet man 80% von 75%?"
.... Die Frage ist für mich also nur: woher weiß ich dass mit dem einen Jahr zum Kalb und einem Jahr zum erwachsen Tier? Ist meine oben genannte "Lösung" richtig?