zwei Vektoren sind dann orthogonal zueinander, wenn das Skalarprodukt = 0 ist.
Zum Beispiel sind (1|0) und (0|1) orthogonal zueinander, weil
1 * 0 + 0 * 1 = 0
(1|2) und (3|7) dagegen sind nicht zueinander orthogonal, weil
1 * 3 + 2 * 7 ≠ 0 ist.
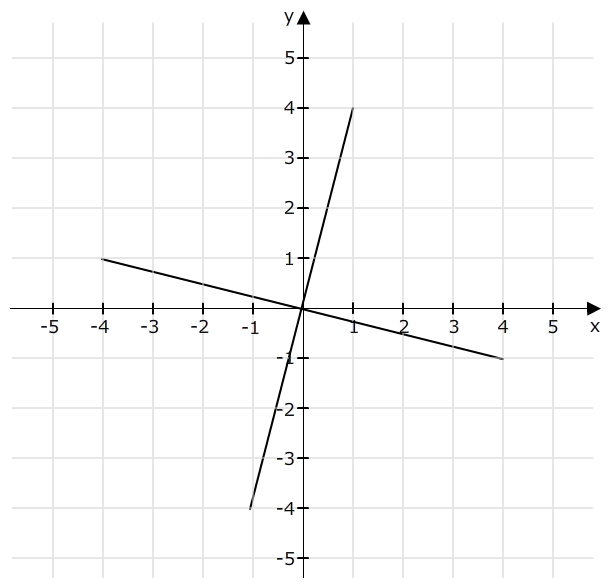
(1|4) und (2|-0,5) sind dagegen wieder orthogonal zueinander, weil
1 * 2 + 4 * (-0,5) = 0
Siehe Skizze:
Das Skalarprodukt wird gebildet, indem man die x-Koordinate von Vektor 1 mit der x-Koordinate von Vektor 2 multipliziert, die y-Koordinate von Vektor 1 mit der y-Koordinate von Vektor 2 multipliziert, die z-Koordinate von Vektor 1 mit der z-Koordinate von Vektor 2 multipliziert usw.
und schließlich all diese Produkte summiert.
Besten Gruß
