Geschlossene Formel für eine Potenzreihe berechnen

Question

Aufgabe:

Bestimme einen geschlossenen Ausdruck für die erzeugende Potenzreihe A(x)
der Folge, gegeben durch die Rekursionsgleichung

a_n − a_n−1 − 3a_n−2 + (n + 1)3ⁿ = 0, für n ≥ 2

mit den Anfangswerten a₀ = 1 und a₁ = 1. (Partialbruchzerlegung und Reihenentwicklung
ist nicht erforderlich).     

Problem/Ansatz:

Wie berechne ich den geschlossenen Ausdruck für die Potenzreihe die vorgegeben ist?

Comments

Warum genau ist das überhaupt eine Potenzreihe? Kennst du dazu einen formalen Hintergrund?

Zur Aufgabe:

Du könntest zuerst mal ein paar Folgenglieder berechnen.

a_n − a_n−1 − 3a_n−2 + (n + 1)3ⁿ = 0, für n ≥ 2

bedeutet.

a_n = a_n−1 + 3a_n−2 - (n + 1)3ⁿ = 0, a0 = 1 und a1 = 1

a_2 = 1 + 3 - 3*3² = 4 - 27 = -23

oder  = 1 + 3 - 3*3² = 1 + 3(1- 3²) = 1 - 3*8 = -23

a_3 = ?

a_4 = ?

---

Müsste nicht a₂=-23 sein?

---

@spacko: Wo ist mein Rechenfehler?

Anfangswerte a0 = 1 und a1 = 1.

---

Beim Auflösen nach a_n scheint ein Vorzeichenfehler vorzuliegen.

---

Danke. Sollte behoben sein.

Answer 1

Lösung a) a(n)=a(n-1)+3*a(n-2)+(n + 1)*3ⁿ {falsch abgeschrieben -> also nicht beachten}

Analog zu https://de.wikipedia.org/wiki/Fibonacci-Folge#Formel_von_Moivre-Bine… kommt man zu
a(n) = a*(1/2 (1 - sqrt(13)))ⁿ + b*(1/2 (1 + sqrt(13)))ⁿ + 3^(n + 1)*n - 2*3^(n + 1)

negative Basis mit (-1)ⁿ = Cos[n*Pi] eliminieren:

f(n) = (1/2 + sqrt(13)/2)ⁿ b - 2 3^(n + 1) + 3^(n + 1) n + (sqrt(13)/2-1/2)ⁿ a cos(n*Pi), f(2) = 31, f(3) = 142

in 2 Gleichungen mit 2 Unbekannten lösen...

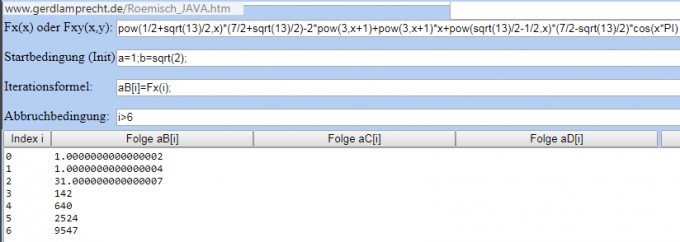
Der Iterationsrechner bestätigt die Richtigkeit der Lösung { x^y = pow(x,y) }:

pow(1/2+sqrt(13)/2,x)*(7/2+sqrt(13)/2)-2*pow(3,x+1)+pow(3,x+1)*x+pow(sqrt(13)/2-1/2,x)*(7/2-sqrt(13)/2)*cos(x*PI)

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@P1/2+@Q13)/2,x)*(7/2+…

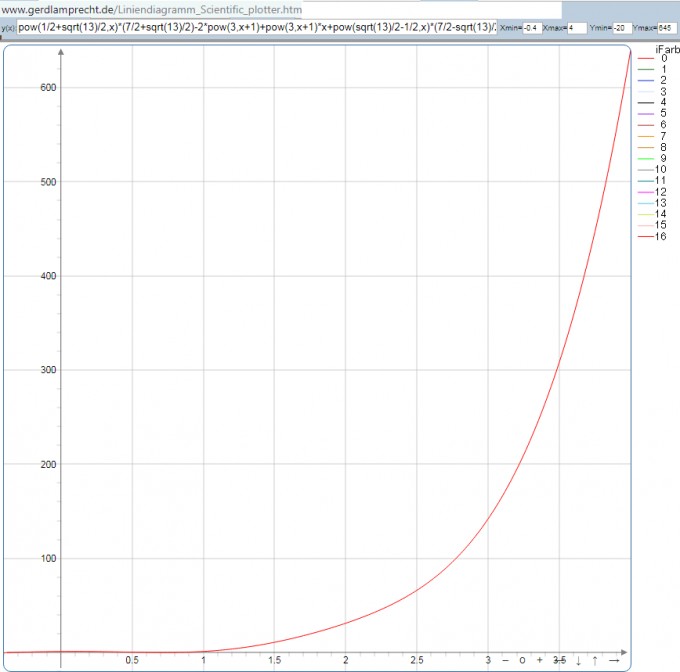
und der Plotter http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm zeigt die weiche (knickfreie) explizite Funktionskurve:

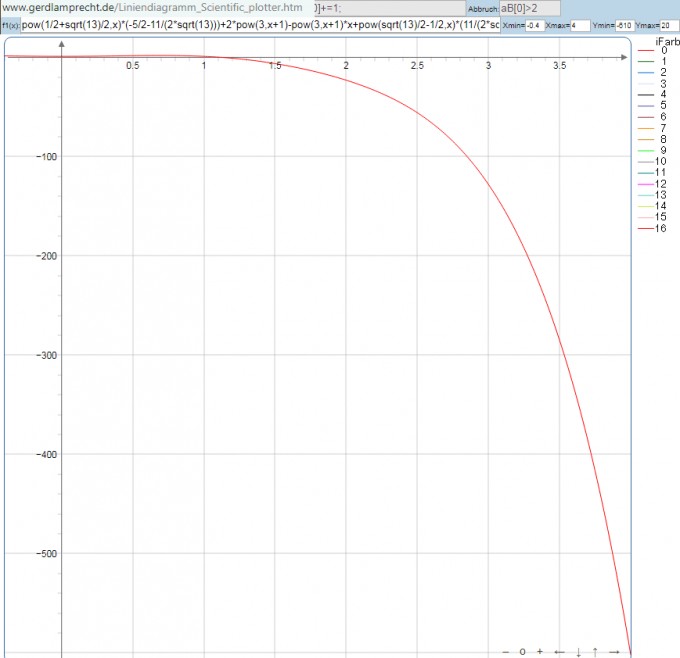
Lösung b) und für negiertes Vorzeichen

a(n)=a(n-1)+3*a(n-2)-(n + 1)*3ⁿ

 negiert sich auch nur der

Teil von - 2 3^(n + 1) + 3^(n + 1) n also

f(n) = (1/2 + sqrt(13)/2)ⁿ (7/2 + sqrt(13)/2) - 2 3^(n + 1) + 3^(n + 1) n + (sqrt(13)/2-1/2)ⁿ (7/2 - sqrt(13)/2)*cos(n*Pi)
f(x)=pow(1/2+sqrt(13)/2,x)*(7/2+sqrt(13)/2)-2*pow(3,x+1)+pow(3,x+1)*x+pow(sqrt(13)/2-1/2,x)*(7/2-sqrt(13)/2)*cos(x*PI)

Probe:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#@P1/2+@Q13)/2,x)*(-5/2…

x | f(x)

0  1
1  1
2  -23
3  -128
4  -602
5  -2444
6  -9353

Comments

Ich hatte in meinem Kommentar einen Vorzeichenfehler beim Auflösen nach a_n. Sollte inzwischen behoben sein.

---

Danke für den Hinweis. Habe das Vorzeichen auch negiert und Lösung b) daraus gemacht.