Hallo Lu. Prinzipiell hast du recht. Grundsätzlich gilt keine Angabe als Mindestens.
Wenn Mama das Kind also fragt ob es ein Bonbon genascht hat und es antwortet "nö", weil es ja 10 waren, dann lügt das böse Kind.
Komischerweise ist das bei einer Lotte-Aufgabe so, dass fast alle Lehrer hier bei keiner Angabe ein genau verlangen.
Vielleicht liegt es daran, dass wenn du 6 richtige hast du auch leider nur den Gewinn für 6 richtige bekommst und nicht noch den für 5 richtige, 4 richtige und 3 richtige.
Zumindest kann ich mir das nur so erklären. Auch eine meiner Schülerinnen, die bei mir gelernt hat, das keine Angabe grundsätzlich mind. heißt und bei einer Lotto Aufgabe die Wahrscheinlichkeit für 4 richtige berechnen sollte hat also berechnet P(X >= 4) so wie sie es von mir beigebracht bekommen hat.
Nach Rückgabe der Arbeit musste sie allerdings mit dem Lehrer diskutieren warum sie eben mindestens 4 Richtige gerechnet hat obwohl doch nicht nach mindestens 4 richtigen gefragt worden war.
Letztlich hat sie die Punkte dennoch bekommen, weil sie das Beispiel mit den Bonbons gebracht hat.
Fazit. Ich empfehle wenn nichts dabei steht, die Lehrkraft zu fragen wie sie die Aufgabe berechnen sollen ob mind. oder genau berechnet werden soll.
Was Lotto betrifft kann man sich bei Wikipedia die Gewinnklassen anstehen.
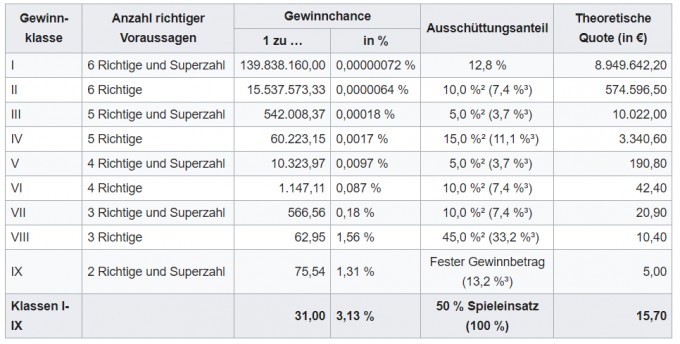
Dort steht eben auch nicht genau 4 Richtige obwohl eben genau das hier berechnet ist.