Aufgabe:
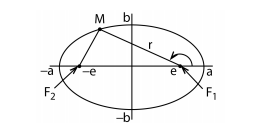
$$\begin{array}{l}{\text { Die Ellipse ist der geometrische Ort aller Punkte } M=(x, y), \text { für die die Summe der Entfernungen zu }} \\ {\text { zwei gegebenen festen Punkten } F_{1}=(e, 0) \text { und } F_{2}=(-e, 0) \text { konstant ist und den Wert } 2 a \text { hat, was der }} \\ {\text { doppelten großen Halbachse a entspricht (vgl. Abbildung). } F_{1} \text { und } F_{2} \text { sind die beiden Brennpunkte }} \\ {\text { einer Ellipse. }}\end{array}$$
$$\begin{array}{l}{\text { a) Drücken Sie die kleine Halbachse } b \text { durch die Größen } a \text { und } e \text { aus. }} \\ {\text { b) } \text { Zeigen Sie mit dem Ergebnis aus a), dass in kartesischen Koordinaten für die Ellipsengleichung }} \\ {\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \text { gilt. }}\end{array}$$$$\begin{array}{l}{\text { c) Bestimmen Sie die Ellipsengleichung in Polarkoordinaten bezüglich des rechten Brennpunkts } F_{1}} \\ { \text { (vgl. Abbildung}), \text { d. } \mathrm{h} . \text { bestimmen sie } r=r(\varphi) . \text { Verwenden Sie dazu die Größen } k=b^{2} / a \text { und }} \\ {\varepsilon=e / a<1 . \text { Die Größe } \varepsilon \text { wird Exzentrizität genannt. }} \\ {\text { d) Bestimmen Sie eine Parameterform }\left(\begin{array}{c}{x} \\ {y}\end{array}\right)=\left(\begin{array}{c}{f(t)} \\ {g(t)}\end{array}\right) \text { der Ellipse. }}\end{array}$$
Problem/Ansatz:
a)
M(x,y), F1(e,0), F2(-e,0)
r1 = Distanz(M,F1) = sqrt((x-e)² + (y-0)²)
r2 = Distanz(M,F2) = sqrt((x+e)² + (y-0)²)
Also gilt wegen r1 + r2 = 2a:
2a = sqrt((x-e)² + (y-0)²) + sqrt((x+e)² + (y-0)²)
Wenn wir nun b herausfinden wollen, nehmen wir den Punkt P(0, b):
2a = sqrt((-e)² + b²) + sqrt(e² + b²) <=> 2a = 2sqrt(e² + b²) <=> a² = e² + b² <=> b = sqrt(a² - e²)
Ist das richtig so?
b)
Jetzt weiß ich nicht wie ich vom Ergebnis b = sqrt(a² - e²) auf die Ellipsengleichung kommen soll.. Würde mich über einen Tipp freuen.
c)
r1² - r2² = 4ex <=> (r2 - r1)(r2 + r1) = 4ex <=> (r2 - r1)2a = 4ex <=> r2 - r1 = 2ex/a
Nach Umformen komme ich dann auf r2 = a + ex/a und r1= a - ex/a
Umrechnung in Polarkoordinaten: r = a - ex/a = a - e/a * (e+rcos(φ)) = a - e²/a - εrcos(φ) = (a² - e²)/a - εrcos(φ) = b²/a - εrcos(φ) = k - εrcos(φ)
Ist das korrekt oder ist da etwas anderes gefragt?
,
MfG