hj2166 hat bereits den entscheidenden Hinweis gegeben. Das lässt sich über vollständige Induktion zeigen. Der Induktionsanfang ist trivial
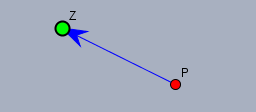
Zwei Städte sind durch eine Einbahnstraße verbunden und die Stadt \(Z\) (wie Ziel) am Ende der Einbahnstraße existiert und ist von der Stadt \(P\) direkt erreichbar.
Beim Übergang von \(n\) auf \(n+1\) Städte liegt bereits ein Szenario vor, bei dem Städte \(P_i\) existieren, von denen man direkt zu einer Stadt \(Z\) kommt und weitere Städte \(Q_i\), deren Weg nach \(Z\) über eine Stadt \(P_i\) zu \(Z\) führt.
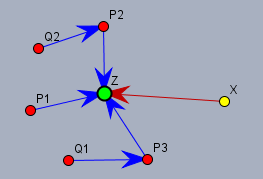
Nun kommt eine weitere Stadt \(X\) hinzu, wobei zunächst zwei Fälle zu unterscheiden sind. Im ersten Fall führt die Straße (rot) von \(X\) nach \(Z\). \(X\) wird dadurch zu einer \(P\)-Stadt mit direkter Verbindung nach \(Z\) und alles ist gut.
Im zweiten Fall geht die Einbahnstraße in die Gegenrichtung, dann sind wieder zwei Fälle zu unterscheiden. Fall 2a liegt vor, wenn man von \(X\) zu mindestens einer \(P\)-Stadt fahren kann (die grüne Straße).
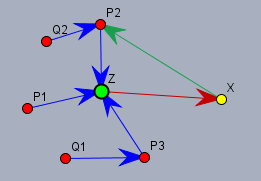
Dann wird \(X\) zu einer \(Q\)-Stadt und wieder ist die Bedingung, dass es eine Stadt \(Z\) gibt, die von jeder Stadt über maximal eine Transferstadt \(P\) zu erreichen ist, erfüllt.
Im Fall 2b kann man von \(X\) aus keine \(P\)-Stadt direkt erreichen. Das heißt aber umgekehrt auch, dass von jeder(!) \(P\)-Stadt eine Einbahnstraße nach \(X\) verläuft.
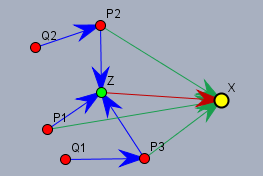
Jetzt wird \(X\) zur neuen \(Z\)-Stadt, zu der alle \(P\)-Städte eine direkte Verbindung haben. Und von allen \(Q\)-Städten aus kann \(X\) über die gleiche Transferstadt erreicht werden, über die man auch zu \(Z\) fahren kann.
Das war's. Melde Dich bitte, falls noch etwas unklar ist.