Hallo MrsMexaMix,
eine Steigung \(s\) in Prozent ist definiert als das Verhältnis von Höhengewinn \(h\) über einer Entfernung \(l\) in der waagerechten
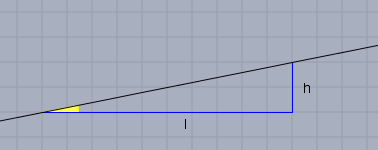
Oben in der Skizze siehst Du eine Steigung (schwarz) mit der Steigung \(s= h/l\). Der Steigungswinkel \(\alpha\) (gelb) ist dann $$\alpha = \arctan\left( \frac hl \right) \quad \Leftrightarrow \quad s = \frac hl = \tan(\alpha) $$Also entspricht ein Steigungswinkel von 1,5° bzw. 2,3°: $$s_{1,5°} = \tan(1,5°) \approx 2,5\% \\ s_{2,3°} = \tan(2,3°) = 4,0\%$$
Wie lang muss eine Hauptstrecke mindestens sein, wenn sie einen Höhenunterschied von 300m überwinden soll?
Es gilt $$s = \frac hl \implies l = \frac hs = \frac {300 \text m}{ \tan(1,5°)} \approx 11,46 \text{km}$$
... mit der Steigung m=1÷11. Gib die Steigung in Prozent und in Grad an.
$$s = \frac 1{11} \approx 0,091 = 9,1\%, \quad \alpha = \arctan\left( \frac 1{11}\right) \approx 5,2°$$ Gruß Werner