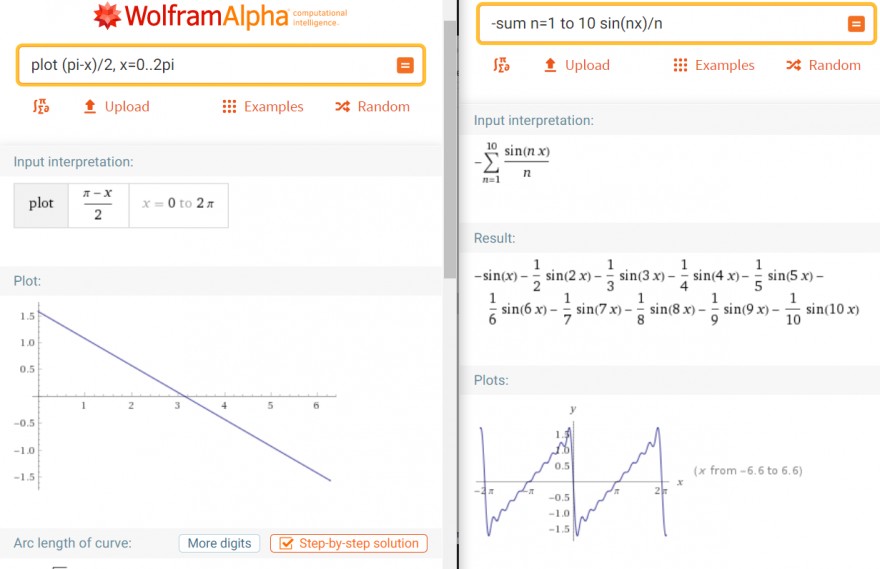
Aufgabe:
Bestimme die Fourierreihendarstellung der Funktion f(x)=\( \frac{π-x}{2} \), x∈(0,2π), welche 2π-periodisch auf ganz ℝ erweitert wird.
Problem/Ansatz:
ich habe die folgenden Fourier-Koeffizienten berechnet:
an=0, bn= -\( \frac{1}{n} \)
Wenn ich mir die so entstandene Fourier-Reihe \( \sum\limits_{n=1}^{\infty}{-\frac{1}{n}sin(nx)} \) bei WolframAlpha plotte sieht das auch "fast richtig" aus (vgl. Bild), ist aber an der x-Achse gespiegelt. Für bn= \( \frac{1}{n} \), also bn positiv, scheint das Ergebnis richtig zu sein.
bn habe ich wie folgt berechnet:
bn=\( \frac{1}{π} \) \( \int\limits_{-π}^{π} \)\( \frac{π-x}{2} \)*sin(nx)dx = \( \frac{π*n*cos(π*n)-sin(π*n)}{π*n²} \) = \( \frac{π*n*cos(π)-sin(π)}{π*n²} \), da n∈ℕ, = \( \frac{π*n*(-1)}{π*n²} \)=\( \frac{-1}{n} \)
Wo könnte sich da ein Fehler eingeschlichen haben?