Na ja das muss aber weiter gehen r=?
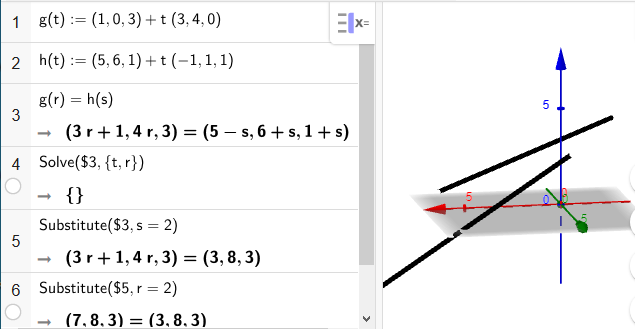
Du siehst, die Geraden sind windschief und wenn man auch r ausrechnet
(5)===> 4 r=8 ===> r=2
ergibt sich auch ein Widerspruch...
BTW: Du kannst Bilder einfach per copy&paste einfügen (vorher bitte zuschneiden oder kleiner rechnen)