obere und untere Schranke von Folgen

Question

Aufgabe:

Bestimme eine untere und eine obere Schranke für x_n= \( \frac{5n-3}{3n-5} \)

Problem/Ansatz:

Ich habe bereits herausgefunden, dass x_n fallend ab n=2 ist, daraus habe Ich geschlussfolgert, dass eine obere Schranke 7 ist, denn x₂ = 7.

Außerden bin Ich mir der Definition der Schranken bewusst:

x_n < s_o und x_n > s_u

Jetzt setzte Ich die 7 ein und bekomme für \( \frac{5n-3}{3n-5} \)  < 7 nach der Fallunterscheidung n ≥ 2 und n ≤ 2 raus. Was aber bedeutet das nun? Ist es richtig? Wenn nein, woran erkenne Ich die richtige Lösung?

Answer 1

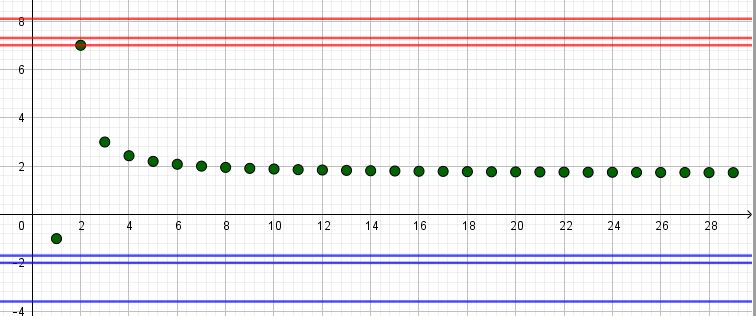
Warum willst du jetzt noch "7 einsetzen"?

Du hast mit 7 eine obere Schranke gefunden. Du hast hier sogar mehr gemacht, als gefordert war: Du hast die KLEINSTE obere Schranke angegeben und begründet, dass es eine solche ist.

Kümmere dich jetzt um eine mögliche untere Schranke (oder von mir aus gleich um die größte untere Schranke.

Bestimme für die ab n=2 fallende Folge doch mal den Grenzwert für n gegen unendlich. Entweder dieser Grenzwert oder der aus der Art geschlagene Wert a1 ist die größte untere Schranke.

Ich habe dir mal die ersten Werte der Folge, drei obere und drei untere Schranken eingeblendet.

Answer 2

Aloha :)$$x_n=\frac{5n-3}{3n-5}=\frac{5}{3}\cdot\frac{3}{5}\cdot\frac{5n-3}{3n-5}=\frac{5}{3}\cdot\frac{3(5n-3)}{5(3n-5)}=\frac{5}{3}\cdot\frac{15n-9}{15n-25}$$$$\phantom{x_n}=\frac{5}{3}\cdot\frac{15n-25+16}{15n-25}=\frac{5}{3}\left(\frac{15n-25}{15n-25}+\frac{16}{15n-25}\right)=\frac{5}{3}\left(1+\frac{16}{5(3n-5)}\right)$$$$\phantom{x_n}=\frac{5}{3}+\frac{5\cdot16}{3\cdot5\cdot(3n-5)}=\frac{5}{3}+\frac{16}{9n-15}$$Wir erkennen sofort, dass \(n=1\) der einzige Wert ist, für den \(9n-15\) negativ ist (nämlich \(=-6\)), für alle anderen \(n\in\mathbb{N}\) ist der Nenner positiv. Das heißt:

Minimum: \(x_1=\frac{5}{3}+\frac{16}{-6}=\frac{10}{6}-\frac{16}{6}=-1\)

Für \(n\ge2\) ist der Nenner \(9n-15\) immer positiv und wächst streng monoton mit zunehmendem \(n\). Dadurch wird der Bruch \(\frac{16}{9n-15}\) mit zunehmendem \(n\) immer kleiner und konvergiert für \(n\to\infty\) gegen \(0\). Daher gilt:

Maximum: \(x_2=\frac{5}{3}+\frac{16}{3}=\frac{21}{3}=7\)

Answer 3

obere: 12984612345178457891256649

untere: -135126419740912634580126508