Kreis- und Geradengleichung Berührpunkte P1 und P2 der Tangenten an den Kreis

Question

geg. :   K: $x^{2}$ +$y^{2}$ - 6x - 2y - 15 = 0 , g: y=-3/4x+1

ges. : Berechnen Sie die Berührpunkte P1 und P2 der Tangenten an den Kreis, die parallel zu g verlaufen und wie lautet die Gleichung der Tangenten.

Mein Ansatz:

Man benötigt erstmal eine Hilfsgerade, also h: y=-3/4x+n

Jetzt habe ich die gerade in K eingesetzt : K: x² + (-3/4x+n)²- 6x - 2*(-3/4x+n) - 15 = 0

und dann bis hier umgeformt : x²-24/25 nx + 16/25 n² - 84/25x - 32/25n -48/5 = 0

Jetzt komme ich nicht weiter. Ich muss doch die Diskriminante gleich Null setzten, aber wie ??

Answer 1

Aloha :)

Wir schreiben zunächst die Kreisgleichung etwas um:$$K:\;0=x^2+y^2-6x-2y-15=(x^2-6x+9)-9+(y^2-2y+1)-1-15$$$$K:\;(x-3)^2+(y-1)^2=25$$Der Kreis hat also den Mittelpunkt $M(3|1)$ und den Radius $R=5$.

Jetzt schreiben wir die Geradengleichung um:$$g:\;\binom{x}{y}=\binom{x}{\frac{3}{4}x+1}=\binom{0}{1}+x\binom{1}{\frac{3}{4}}$$Man erkennt den Richtungsvektor der Geraden. Dazu gibt es zwei senkrechte Vektoren$$\vec v_1=\binom{-\frac{3}{4}}{1}\quad;\quad \vec v_2=\binom{\frac{3}{4}}{-1}$$wobei beide die Länge $\sqrt{1+\frac{9}{16}}=\frac{5}{4}$ haben.

Damit können wir die Berührpunkte bestimmen:

$$\vec p_1=\vec m+\frac{R}{5/4}\vec v_1=\binom{3}{1}+\frac{5}{5/4}\binom{-\frac{3}{4}}{1}=\binom{3}{1}+4\binom{-\frac{3}{4}}{1}=\binom{0}{5}$$$$\vec p_2=\vec m+\frac{R}{5/4}\vec v_2=\binom{3}{1}+\frac{5}{5/4}\binom{\frac{3}{4}}{-1}=\binom{3}{1}+4\binom{\frac{3}{4}}{-1}=\binom{6}{-3}$$Also haben wir: $P_1(0|5)\;;\;P_2(6|-3)$.

Die Gleichungen der Tangenten sind nun:$$t_1:\;\vec x_1=\binom{0}{5}+x\binom{1}{\frac{3}{4}}\quad;\quad t_2:\;\vec x_2=\binom{6}{-3}+x\binom{1}{\frac{3}{4}}=\binom{0}{-7,5}+x\binom{1}{\frac{3}{4}}$$Das kann man auch als Funktionsgleichungen schreiben:

$$t_1:\;\vec x_1=\binom{x}{5+\frac{3}{4}x}\quad;\quad t_2:\;\vec x_2=\binom{x}{-7,5+\frac{3}{4}x}$$$$t_1:\;y=5+\frac{3}{4}x\quad;\quad t_2:\;y=-7,5+\frac{3}{4}x$$

Answer 2

Zusammenfassen und pq-Formel anwenden. Diskriminante ist der Term unter der Wurzel. Aber das Einsetzen ist fehlerhaft.

x²+(-3/4x+1)²-6x-2(-3/4+1)-15=0

Comments

Wie soll ich das noch weiter zusammenfassen ?

---

Es sollte heißen:

x²+(-3/4x+n)²-6x-2(-3/4x+n)-15=0

Klammern auflösen:

x²+9/16x²-3/2xn+n²+6x+3/2x-2n-15=0

jetzt alles mit x², mit x und alles ohne x zusammenfassen

---

Da bekomme ich : 25/16x² - 3/2xn + n² - 9/2x - 2n - 15 = 0

---

ich bekomme:

25/16·x²+(15+3n)/2·x+2n-15=0  |·25/16

Dann pq-Formel.

Answer 3

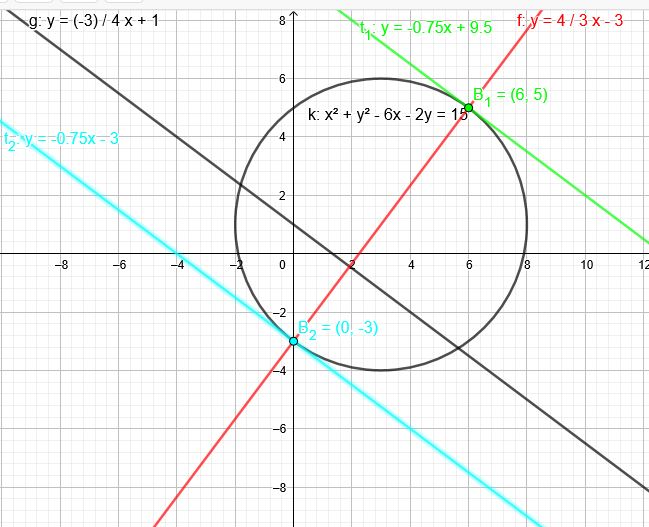
geg. : K: $x^{2} + y^{2} - 6x - 2y =15$        g: $y=\red{-\frac{3}{4}}x+1$

Lösung mittels impliziter Differenzierung:

 $k(x,y)= x^{2} + y^{2} - 6x - 2y -15$ 

$k_x(x,y)= 2x - 6$

$k_y(x,y)= 2y - 2$

$k'(x)= -\frac{k_x(x,y)}{k_y(x,y)}=-\frac{ x - 3}{y - 1}$

$\red{-\frac{3}{4}}=-\frac{ x - 3}{y - 1}$

$\frac{3}{4}=\frac{ x - 3}{y - 1}$

$y=\frac{4}{3}x-3$

Diese Gerade schneidet den Kreis in den beiden Berührpunkten. Dann die Tangenten aufstellen.

Answer 4

Der Kreismittelpunkt wurde dir mit (3 | 1) bereits berechnet. Berechne dann die Schnittpunkte einer Geraden h durch M senkrecht zu g mit dem Kreis.

h(x) = 4/3·(x - 3) + 1 = 4/3·(x - 3) + 1 = 4/3·x - 3

Also in K einsetzen

x² + (4/3·x - 3)² - 6·x - 2·(4/3·x - 3) - 15 = 0 --> x = 6 ∨ x = 0

Damit brauchen wir noch die y-Koordinaten durch einsetzen in h

h(0) = -3 → (0 | -3)
h(6) = 5 → (6 | 5)

Das sind die Punkte in denen du die Tangente aufstellst

t1(x) = - 3/4·(x - 0) - 3 = -3/4·x - 3
t2(x) = - 3/4·(x - 6) + 5 = 19/2 - 3/4·x

Skizze

Plotlux öffnen

f₁(x) = 1+√(-x²+6x+16)f₂(x) = 1-√(-x²+6x+16)f₃(x) = -3/4x-3f₄(x) = 19/2-3/4xZoom: x(-12…12) y(-9…9)

Comments

Wenn du das auch noch über dein Verfahren haben möchtest bei dem die Determinante auf Null gesetzt wird, kannst du dich nochmals melden.