Text erkannt:
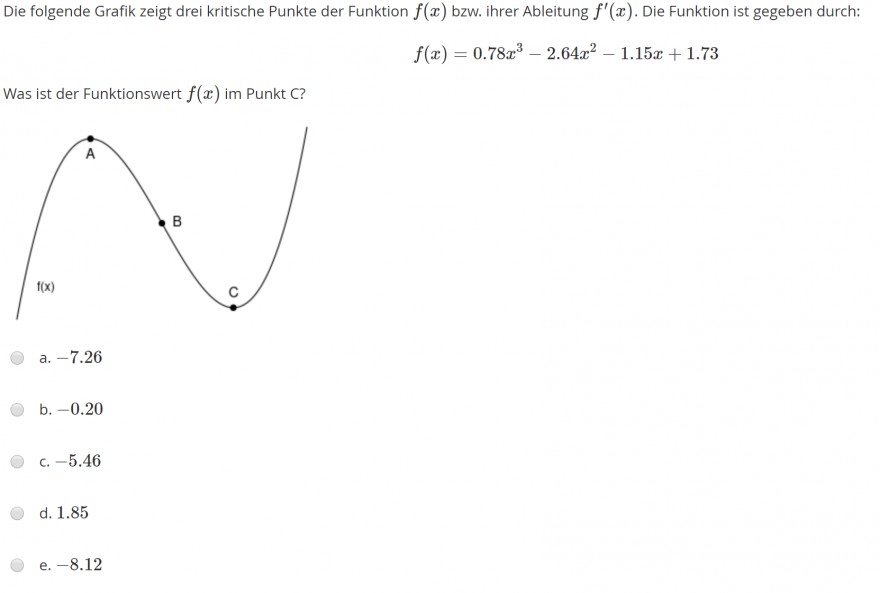
Die folgende Grafik zeigt drei kritische Punkte der Funktion \( f(x) \) bzw. ihrer Ableitung \( f^{\prime}(x) \). Die Funktion ist gegeben durch: Was ist der Funktionswert \( f(x) \) im Punkt \( C \) ? \[ f(x)=0.78 x^{3}-2.64 x^{2}-1.15 x+1.73 \] a. -7.26 b. -0.20 c. -5.46 tw) d. 1.85 e. -8.12
Was mache ich falsch:
1. Ableitung = 0 setzen,
kleinere xWert nehmen x = -0.200064
2. Ableitung
-.200064 für x einsetzen.
Mein Ergebnis -6.216
Bitte um Hilfe