Aufgabe:
a) Sei n ∈ N und σ ∈ Sn eine beliebige Permutation. Zeigen Sie, dass σ sich als Produkt von
Transpositionen der Form (i, i + 1) schreiben lässt, wobei i ∈ {1, . . . , n − 1}.
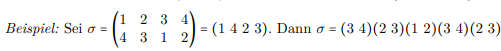
Hinweis: Sie können annehmen, dass σ eine Transposition ist. Diese Aufgabe ist die Grundlage
von Bubblesort.
b) Sei n ∈ N. Eine Permutation σ ∈ Sn heißt gerade, wenn das Signum ε(σ) = 1. Andernfalls (d.h.
falls ε(σ) = −1) heißt σ ungerade. Zeigen Sie: Für n > 1 enthält Sn genauso viele gerade wie
ungerade Permutationen.
Hinweis: Wenden Sie die Leibnizsche Summenformel auf eine geeignete Matrix an
Ich bin mir irgendwie total unschlüssig, wie ich an die Sache heran gehen soll. Wäre cool, wenn mir jemand helfen könnte :)