Aufgabe:
Definition Konvexität …
Problem/Ansatz:
! Gegeben ist folgende Definition zur Konvexität einer Funktion:
Es sei D ⊂ ℝ ein Intervall. Eine Funktion f: D → ℝ heißt konvex, falls für alle x1,x2 ∈ D und alle 0 < λ < 1 immer gilt:
f( λx1 + (1- λ)x2) ≤ λf(x1)+(1- λ)f(x2)
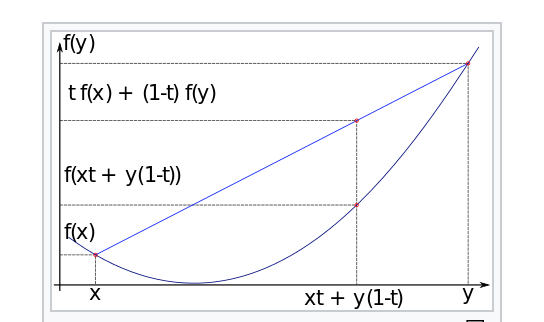
Nun zu meinem Problem: Das eine Funktion f: D → ℝ konvex ist, bedeutet ja, dass ich zwei beliebige Punkte f(x1) und f(x2) mit x1 und x2 ∈ D durch eine Sekante miteinander verbinden kann und für jeden Punkt x3 ∈[x1,x2] gilt: f(x3) befindet sich unter dieser Sekante oder liegt genau auf dieser Sekante. Wenn man die Anschauung unten betrachtet, dann stellt x3 ja irgendeine Zahl zwischen x und y dar, die sich darstellen lässt als xt+(1-t)y. Hier meine erste Frage: wie genau kommt man darauf, dass jede Zahl zwischen x und y genau so darstellbar ist? Dann zu meiner zweiten Frage: Es scheint ja der Fall zu sein, dass man mit tf(x)+(1-t)f(y) immer einen Punkt trifft, der denselben Wert auf der X-Achse hat, wie f(xt+y(1-t)) und der zusätzlich auf der Sekante liegt, die f(x) und f(y) verbindet. Weshalb ist das so?
!