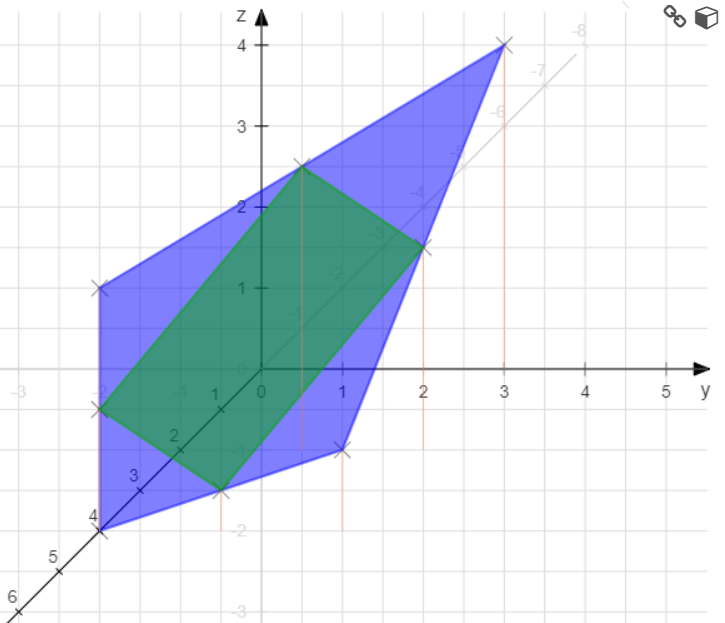
Prüf mal bitte die Koordinaten der Punkte. Das sieht komisch aus.
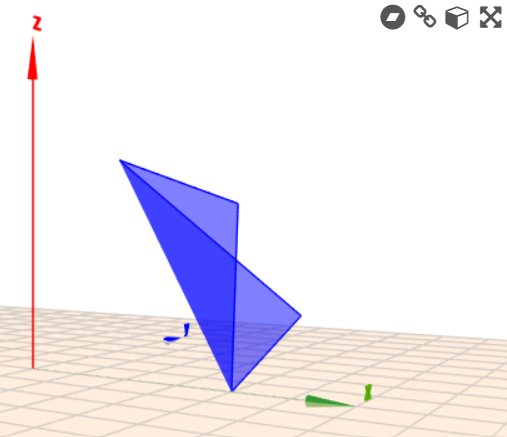
Ok. Die Punkte sollen wohl so richtig sein. Das ist halt ein Raumviereck.
Die Seitenmitten sind dann
MAB = [4, 1.5, 0.5]
MBC = [2, 3, 2.5]
MCD = [2, 1.5, 3.5]
MAD = [4, 0, 1.5]
MAB_MBC = [-2, 1.5, 2]
MCD_MAD = [2, -1.5, -2]
MBC_MCD = [0, -1.5, 1]
Gegenüberliegende Seiten sind parallel und Gleich lang. Eine weitere Seite ist nicht parallel und damit hat man ein Parallelogramm.
Die normale Schrägbildzeichnung ist etwas trügerisch, weil man nicht erkennt das es sich nicht um ein ebenes Viereck handelt.