Bestimmen Sie den Punkt P, in dem die Tangente parallel zur Geraden y = 2x ist.

Question

Aufgabe:

Gegeben ist die Funktion f mit f(x) = -1/2 x² + 2x - 2. Bestimmen Sie den Punkt P, in dem die Tangente parallel zur Geraden y = 2x ist.

Comments

hallo , bestimmen geht auch grafisch

Plotlux öffnen

f₁(x) = -0,5x²+2x-2f₂(x) = 2xf₃(x) = 2x-2

---

hallo , bestimmen geht auch grafisch

Und wie willst du grafisch einen Punkt wie -sagen wir mal-

(0,00359 | -2,0005723) oder ($\sqrt{17}|\frac{13}{9} )$ bestimmen?

---

Und wie willst du grafisch einen Punkt wie -sagen wir mal-
(0,00359 | -2,0005723) oder ($\sqrt{17}|\frac{13}{9} )$ bestimmen?

Ganz einfach! Gegeben ist die Parabel, also auch ihr Brennpunkt $F(2|\, -0,5)$ und ihre Leitlinie (blau gestrichelt) bei $y=0,5$. Weiter ist eine Gerade mit beliebiger Steigung durch den Ursprung gegeben (die blaue Gerade durch $O$).

Aufgabe:

Bestimmen Sie den Punkt P, in dem die Tangente parallel zur Geraden y = mx ist.

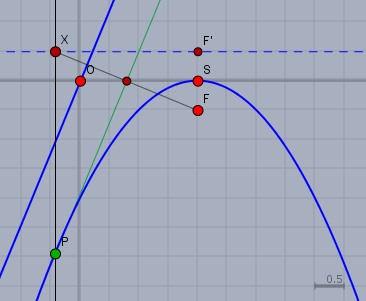
Fälle von $F$ das Lot auf die Ursprungsgerade (blau). Das Lot schneidet die Leitlinie in $X$. Das Lot in $X$ zur Leitlinie schneidet die Mittelsenkrechte von $XF$ in $P$ (der grüne Punkt).

---

schneidet die Mittelsenkrechte von $XF$ in $P$ (der grüne Punkt).

Und genau da setzte meine Frage an: Wie willst du denn an einem (gezeichneten) Punkt ablesen, ob da nun eine Koordinate den Wert -2 oder doch nur den Wert -2,0005723 hat?

---

Und genau da setzte meine Frage an: Wie willst du denn an einem (gezeichneten) Punkt ablesen, ..

Du 'liest ihn ab', indem Du drauf guckst. Der Punkt ist konstruiert und damit graphisch eindeutig bestimmt. Das ist eine graphische Lösung! Was kümmern mich seine Koordinaten ;-)

Diese vielen Stellen hinterm Komma werden eh' überbewertet! Und exakt ist es u.U. genauso wenig wie eine graphische Lösung.

---

Vom Duplikat:

Titel: Bestimmen Sie den Punkt P, in dem die Tangente parallel zur Geraden y=2x ist.

Stichworte: potenzen

Aufgabe:

Gegeben ist die Funktion f mit f(x) = -1/2x²+2x-2.

Problem/Ansatz:

Bestimmen Sie den Punkt P, in dem die Tangente parallel zur Geraden y=2x ist.

---

Doppelposts sind nicht gut. Warum reagierst du nicht auf die Antworten zu deinem ersten Post?

Answer 1

f(x)=-1/2x²+2x-2

g(x)=2x hat die Steigung m=2

f ´( x )=  - x +2

-x+2= 2

x=0→f(0)=-2

B(0|-2)

mfG

Moliets

Comments

Wenn ich so vorgehe wie bei

https://www.mathelounge.de/769701/punkt-bestimmen-graph

ergibt sich :

f(x)=  - 1/2  x² + 2x - 2  und g(x) = 2 x

- 1/2  x² + 2x - 2=2x

1/2  x²  +2 =0

x² =   - 4 =  4  i²

(x -0) ^ 2= 4 i²

x_1=0 + 2 i

x_2= 0- 2 i

B(0|-2)

mfG

Moliets

Answer 2

f'(x) = 2 --> x = 0

f(0) = -2 → P(0 | -2)

Tangente

t(x) = f'(0)·(x - 0) + f(0) = 2·x - 2

Skizze

Plotlux öffnen

f₁(x) = -1/2x²+2x-2f₂(x) = 2x-2