Moin Leute, hat jemand eine Idee, wie man hier integiert? Danke euch !
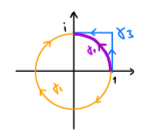
(a) Berechnen Sie das Integral \( \int \limits_{\gamma_{j}} \frac{1}{z} \mathrm{~d} z \) für die drei Wege \( \gamma_{1}, \gamma_{2}, \gamma_{3} \) von 1 nach \( i, \) die in folgendem Bild dargestellt sind:
(b) Berechnen Sie das Integral
\( \int \limits_{\gamma} z e^{z^{2}} \mathrm{~d} z \)
für den Weg \( \gamma \), welcher die Punkte 0 und \( 1+i \) entlang der Parabel \( y=x^{2} \) verbindet.