Gruppen. definieren und prüfen

Question

Prüfen Sie, ob folgende Vorschriften Gruppenhomomorphismen definieren.

φ:(Z,+)→(Q\{0},·),n→2 .
(b) φ:(R,+)→(R,+),a→a+1.
(c) φ: ((Z/mZ)×,·) → (Z/mZ,+),a → a mit m ≥ 2

(d) Prüfen Sie, für welche n ∈ N mit n ≥ 2 die Abbildung ein gruppenhomomorph. def.

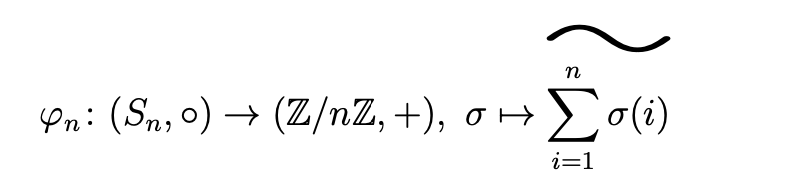
Prüfen Sie, ob folgende Vorschriften Gruppenhomomorphismen definieren.

Answer 1

a) nicht lesbar

b) ist keiner, da φ(3) = 4  und φ(5) = 6

aber φ(3+5) = 9 ≠ 4 + 6

c) ist auch keiner, da z.B. für m=7 gilt

φ(3) = 3  und φ(2) = 2

aber φ(3*2) =  6 ≠ 3+2

Comments

aber wieso? ich verstehe nich woran du das erkannt hast, wie hast du es geprüft

---

Was geprüft ?

---

wir sollen ja prüfen wieso die vorschriften gruppenhomo. sind wie hast du das denn erkannt

---

Aber das sind ja keine. Hab einfach mal ein

paar Beispielzahlen eingesetzt.

---

aber wie schreibe ich dass denn richtig auf. a,b,c und d sind alle keine?

---

So wie ich es auch gemacht habe:

Widerlegen durch ein Gegenbeispiel

---

aber ich kann das doch nicht einfach so hinschreiben oder? also kannst du mir a ausfürhlich aufschreiben und ich schreibe b c d und du schaust b ich es verstanden habe? und ist d ein gruppenh.

---

b) ist kein Homomorphismus er,

da φ(3) = 4  und φ(5) = 6

Wäre es ein Homomorphismus, dann müsste

gelten φ(3+5)  = φ(3)  + φ(5)

aber φ(3+5) = 9 ≠ φ(3)  + φ(5)  = 10

---

ja das habe ich verstanden aber ist d ein gruppenhomo. oder nicht? ich verstehe diese linie über das summenzeichen auch nicht