a)Kann mir jemand hierbei helfen? Wie kann man das ganze verallgemeinert mit x und y darstellen?
b) mit der b kann ich leider gar nichts anfangen
Aufgabe:
In der Grundschule wird das Aufgabenformat , Wer trifft die \( 50 ?^{\prime \prime} \) eingesetzt.
Summe: 50
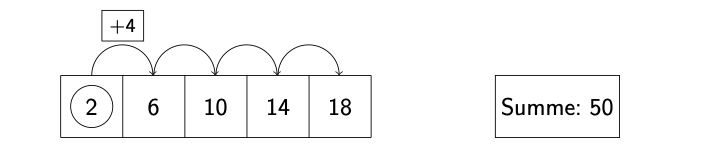
Hierbei wird eine \( _{n} \) Startzahl" im ersten Kreis (hier 2 ) gewählt und zusätzlich eine , Additionszahl" über dem ersten Pfeil im Kasten festgelegt (hier 4). Die Additionszahl wird nun zur Startzahl addiert und das Ergebnis ins Feld rechts neben diese geschrieben. Dann wird die Additionszahl wiederum zu dem Ergebnis (hier 6 ) addiert und ins Feld daneben geschrieben. So wird auch in den weiteren Feldern vorgegangen.
Wenn alle fünf Felder der Zahlenreihe mit den jeweiligen Ergebnissen ausgefüllt sind, werden alle Zahlen addiert und die Summe der Zahlen, die , Zielzahl", im äußeren rechten Feld notiert (hier 50 ).
Wir betrachten nun das Spiel , Wer trifft die \( 50 ?^{\prime\prime}-\mathrm{d} . \mathrm{h} . \) die Zielzahl muss 50 sein.
a) Wie sieht die Aufgabe für eine beliebige Startzahl \( x \) und eine beliebige Additionszahl \( y \) aus? Verwenden Sie dazu die obige Darstellung.
(b) Bestimmen Sie alle Lösungen von , Wer trifft die \( 50 ?^{\prime\prime}, \) sofern wir als Start- und Additionszahl nur Werte aus \( \mathbb{N}_{0} \) erlauben.