Für welche x element aus Reelle Zahlen positiv ist f(x) g(x)?

Question

Aufgabe: Gegeben sind die Funktionen f: Reelle Zahlen positiv -> reelle Zahlen. Für welche x element aus Reelle Zahlen positiv ist f(x)< g(x)? Wir berechne ich sowas?

Problem/Ansatz:

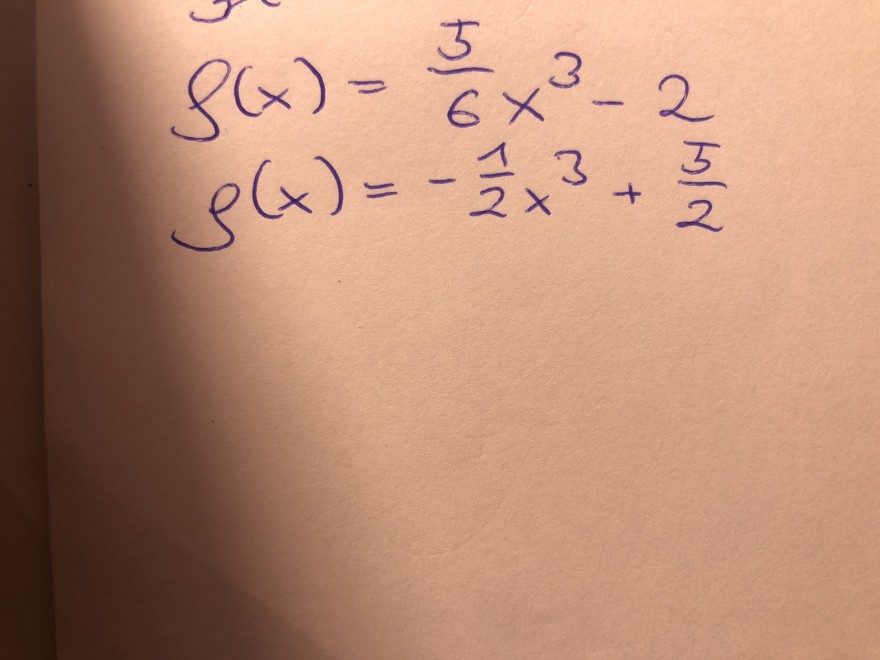
Text erkannt:

$f(x)=\frac{5}{6} x^{3}-2$
$\rho(x)=-\frac{1}{2} x^{3}+\frac{5}{2}$

Answer 1

f(x)= 5/6x³ - 2

g(x)=-1/2x³+5/2

f(x)<g(x)

$\frac{5}{6}$  x^3  - 2 <  - $\frac{1}{2}$  x^3 + $\frac{5}{2}$ |*6

5x³  - 12  <  - 3x³ + 15

8 x³  < 27

x^3 <$\frac{27}{8}$

x < $\frac{3}{2}$

mfG

Moliets

Text erkannt:

$\equiv$ GeoGebra Classic
$f(x)=\frac{5}{6} x^{3}-2$
$g(x)=-\frac{1}{2} x^{3}+\frac{5}{2}$
$a: x<\frac{3}{2}$
:
Eingabe...