Text erkannt:
\( \begin{aligned}\{f: \mathbb{R} \longrightarrow \mathbb{R} \mid f(-x)&=f(x)\} \subset(V,+, \cdot), \text { wobei } V=\{f: \mathbb{R} \longrightarrow \mathbb{R}\} \text { und } \\ & f+g: \mathbb{R} \longrightarrow \mathbb{R}, \quad(f+g)(x)=f(x)+g(x) \\ & s \cdot f: \mathbb{R} \longrightarrow \mathbb{R}, \quad(s \cdot f)(x):=s \cdot f(x) \end{aligned} \)
Aufgabe:
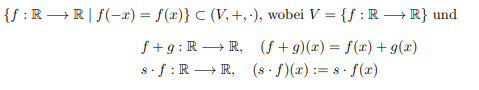
Problem/Ansatz:
Ich weiß leider nicht, wie ich hier die Bedingungen zeigen soll.