Bestimmen Sie f(x) in Hauptform.

Question

Aufgabe:

Für eine quadratische Funktion f gilt f(2)=0,5; Das Schaubild K der Funktion f hat eine doppelte NST in x =2. Bestimmen Sie f(x) in Hauptform.

Problem/Ansatz:

Wie kann ich darauf kommen? Ich brauche es gerade dringend aber komme nicht drauf

Answer 1

Wenn bei 2 eine Nullstelle ist, hat f dort den Wert 0 und nicht den Wert 0,5.

So eine Funktion gibt es nicht.

Answer 2

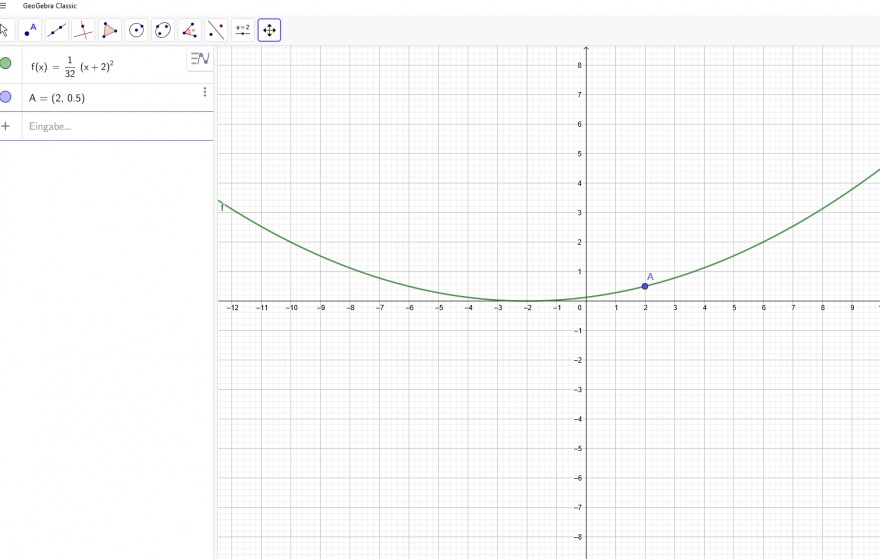
Wenn die doppelte Nullstelle bei x=-2 liegt, funktioniert es:

Text erkannt:

Geobiten
\( f(x)=\frac{1}{32}(x+2)^{2} \)
\( \mathrm{A}=(2,0.5) \)
\( +\quad \) Eingabe...

f(x)=  a* (x+2)^ 2

f(2)=0,5

f(2)=  a* (2+2)^ 2

a* (2+2)^ 2=0,5

a=\( \frac{1}{32} \)

f(x) =  \( \frac{1}{32} \) *(x+2)^ 2

Nun ausmultiplizieren zur Hauptform.