Hallo die Aufgabe befindet sich im Anhang.
Ich weiß nicht genau wie ich das zeigen soll, in der Aufgabe steht bereits das k < l ist und somit ist ja klar das es dann nicht gleich sein kann. 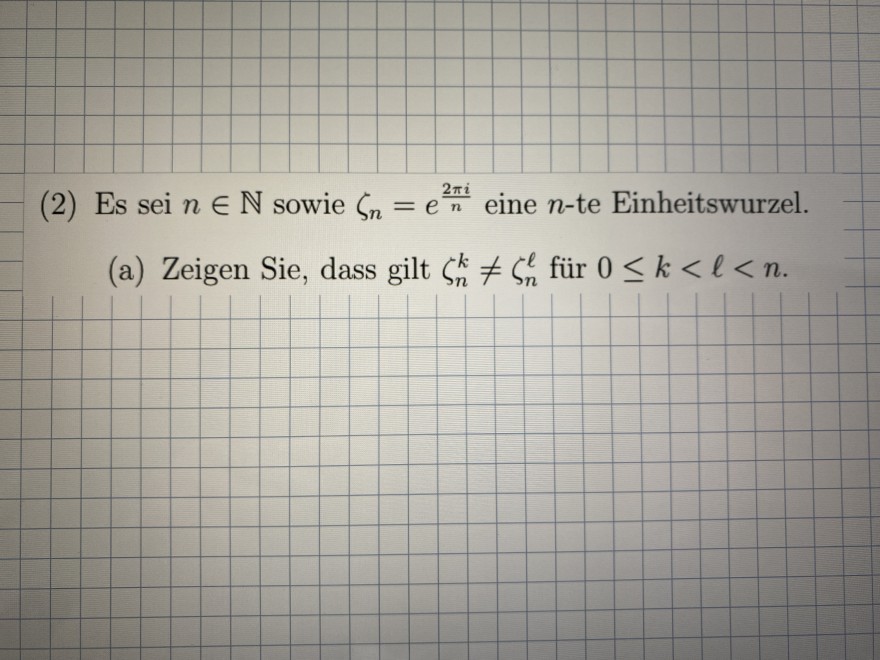
Text erkannt:
(2) Es sei \( n \in \mathbb{N} \) sowie \( \zeta_{n}=e^{\frac{2 \pi i}{n}} \) eine \( n \) -te Einheitswurzel.
(a) Zeigen Sie, dass gilt \( \zeta_{n}^{k} \neq \zeta_{n}^{\ell} \) für \( 0 \leq k<\ell<n \).