Berechnen Sie, wie viele Telefonleitungen mindestens geschaltet werden müssen, damit die Wahrscheinlichkeit einer …

Question

Aufgabe:

Bei der Telefon-Hotline der Fluggesellschaft gehen pro Stunde etwa 120 Anfragen ein, die durchschnittlich 10 Minuten dauern. Berechnen Sie, wie viele Telefonleitungen mindestens geschaltet werden müssen, damit die Wahrscheinlichkeit einer freien Leitung für einen Anrufer größer als 90% ist.

Problem/Ansatz:

Also ich hab bis jetzt aufgeschrieben, dass

n=120

p=1/6

Dann hab ich mir noch gedacht, dass eine Person ja ca 6 Telefonate pro Stunde schafft und deswegen für k erstmal 20 eingesetzt.

Allerdings weiß ich nicht genau wie ich weitermachen muss.

Comments

Wie kommst Du auf p = 1/6?

Was für eine Verteilung nimmst Du für die eintreffenden Telefonanrufe? Kennst Du Siméon Denis Poisson? Ich menie nicht persönlich, der ist nämlich schon tot.

---

Also eine Stunde hat ja 60 Minuten und ein Telefonat dauert um die 10 Minuten also dachte ich das p=10/60=1/6 ist

---

Ich verstehe nicht, was dann die Bedeutung der so ausgerechneten Wahrscheinlichkeit sein soll.

---

1/6 ist die Wahrscheinlichkeit das ein Anrufer in einer bestimmten Minute einer Stunde durch seinen Anruf eine Leitung belegt.

---

In einer bestimmten Minute, achso. Wenn das heute so unterrichtet wird, dann kann ich nicht mitreden.

---

Ob das jetzt eine bestimmte Minute oder eine bestimmte Sekunde ist, ist auch recht unerheblich für die Berechnung.

Answer 1

Ich mache das mal näherungsweise über die Binomialverteilung wie das in der Oberstufe normal gemacht wird.

Jede Person belegt zu p = 1/6 eine bestimmte Minute einer Stunde

Es rufen n = 120 Personen pro Stunde an

Man macht sich mal eine WK-Verteilung

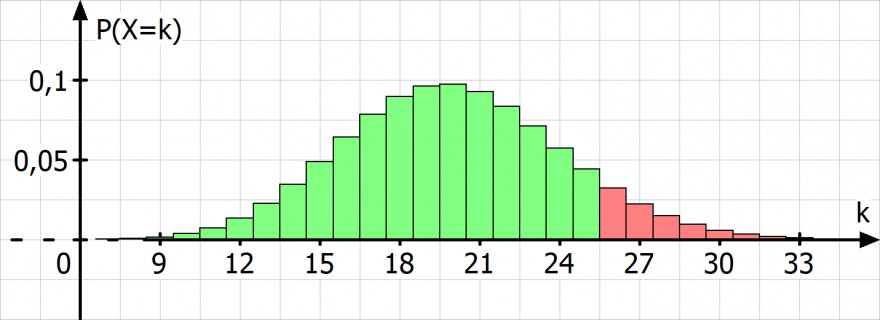
25 Anrufleitungen sollten also auslangen. Denn die Wahrscheinlichkeit das eine Minute von hochstens 25 Personen belegt wird beträgt

P(X <= 25) = 0.9080 und damit langen diese 25 Leitungen zu 90% aus.

Mann kann hier auch andere Verteilungen dafür herbeiziehen. Dann kommen leicht abweichende Ergebnisse heraus.