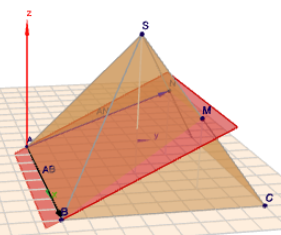
Hallo Hanna,
ist die Spitze also Punkt s jetzt (4/4/6)?
Ja - unter der Annahme, dass die Pyramide regelmäßig und gerade ist und 'oben' da ist, wo die positive Z-Achse hin zeigt, ist das richtig.
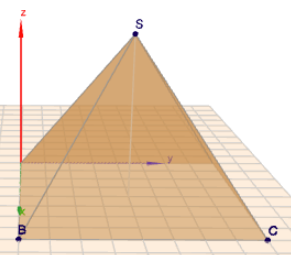
(klick auf das Bild)
Erstelle ich diese aus den normalen Punkten oder aus den Punkten ABMN?
Keine Ahnung, was Du mit 'normalen Punkten' meinst.
Da brauchst für eine Ebene drei Punkte. Es reichen also z.B. die Punkte \(A\), \(B\) und \(N\). Damit bestimmst Du zwei Vektoren$$\vec{AB} = \begin{pmatrix}8\\ 0\\ 0\end{pmatrix}, \quad \vec{AN}= \begin{pmatrix}2\\ 6\\ 3\end{pmatrix}$$und damit wiederum das Kreuzprodukt$$\vec n' = \vec{AB} \times \vec{AN} = \begin{pmatrix}0\\ -24\\ 48\end{pmatrix}$$Da die Ebene durch den Punkt \(A\) - den Ursprung - geht, ist die rechte Seite der Normalenform \(=0\). Die Ebene ist also$$E: \quad \begin{pmatrix}0\\ -24\\ 48\end{pmatrix} \vec x = 0$$das darf man auch noch durch \(24\) dividieren, dadurch ändert sich nichts an der Ebene$$E: \quad \begin{pmatrix}0\\ -1\\ 2\end{pmatrix} \vec x = 0$$es sind etwas gefälligere Zahlenwerte.