Aufgabe:
Geben sie an c,d IR an mit z10 =c+dj zu z=1+j
Problem/Ansatz:
Ich versteh nicht wieso hier aus ejπ 2,5 =ej π 0,5 wird. Wo kommt die 0,5 her und wieso bleibt nur 32j übrig?
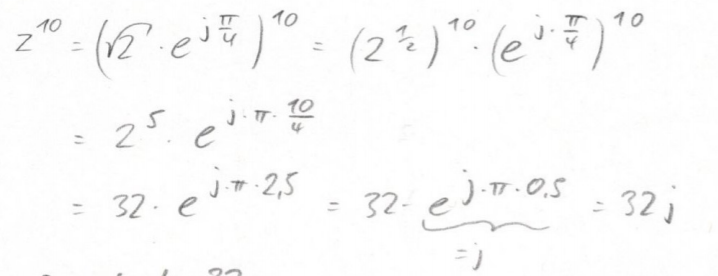
Text erkannt:
\( \begin{aligned} z^{10} &=\left(\sqrt{2} \cdot e^{j \frac{\pi}{4}}\right)^{10}=\left(2^{\frac{1}{2}}\right)^{10} \cdot\left(e^{j \cdot \frac{\pi}{4}}\right)^{10} \\ &=2^{5} \cdot e^{j \cdot \pi \cdot \frac{10}{4}} \\ &=32 \cdot e^{j \cdot \pi \cdot 2,5}=32 \cdot \underbrace{e^{j \cdot \pi \cdot 0,5}}_{j}=32 j \end{aligned} \)