E-funktion per Hand lösen?

Question

Hallo, ich steh gerade aufm Schlauch:

Kann ich

4e^2x + 6e^x - 4 = 0

per Hand lösen?

Answer 1

Hallo,

4e^(2x) + 6e^(x) - 4 = 0

z=e^x

---->

4 z^2 + 6z - 4 = 0 |: 4

z^2 + (3/2) z - 1 = 0 ->pq-Formel

z_1.2= -3/4 ± √ (9/16 +16/16)

z_1.2= -3/4 ± 5/4

z₁= 1/2

z₂= -2

->Resubstitution:

a) e^x= 1/2 | ln(..)

x ln e= ln (1/2) =ln(1) -ln(2)

ln e=1

ln(1)=0

---->

x= -ln(2)

b) e^x= -1/2 ->keine Lösung

Answer 2

Substituieren: e^x= z

4z^2+6z-4=0

z^2+1,5z-1 =0

pq- Formel:

-0,75±√(0,75^+1)

z1 = 0,5

z2 = -2 (entfällt)

e^x=z

x= lnz

x= ln0,5= ln(1/2) = ln1-ln2 = -ln2

Answer 3

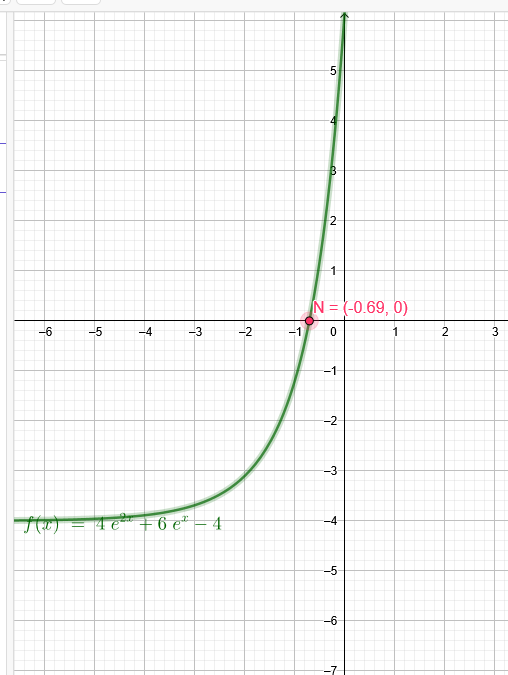
Weg ohne Substitution:

4\( e^{2x} \) + 6\( e^{x} \) - 4 = 0

\( e^{2x} \) + \( \frac{3}{2} \) \( e^{x} \)  = 1

(\( e^{x} \)+\( \frac{3}{4} \))^2 = \( \frac{25}{16} \)|\( \sqrt{} \)

1.)  \( e^{x} \) = -\( \frac{3}{4} \) +\( \frac{5}{4} \)=\( \frac{1}{2} \)

x₁=ln(\( \frac{1}{2} \))≈ - 0,69

2.)  \( e^{x} \) = -\( \frac{3}{4} \) -\( \frac{5}{4} \)=-2   →  keine Lösung in ℝ

Answer 4

Hier gibt es eine Übersicht über Lösungsstrategien für Exponentialgleichungen mit einigen kommentierten Beispielen.