1.) 2x-5y=9 → y=\( \frac{2}{5} \)x-\( \frac{9}{5} \)
2.) 4x+ay=5 → y=-\( \frac{4}{a} \) x + \( \frac{5}{a} \)
\( \frac{2}{5} \)x-\( \frac{9}{5} \)=-\( \frac{4}{a} \) x + \( \frac{5}{a} \)
\( \frac{2}{5} \)x+\( \frac{4}{a} \) x =\( \frac{9}{5} \)+ \( \frac{5}{a} \)
x*(\( \frac{2}{5} \)+\( \frac{4}{a} \)) =\( \frac{9}{5} \)+ \( \frac{5}{a} \)
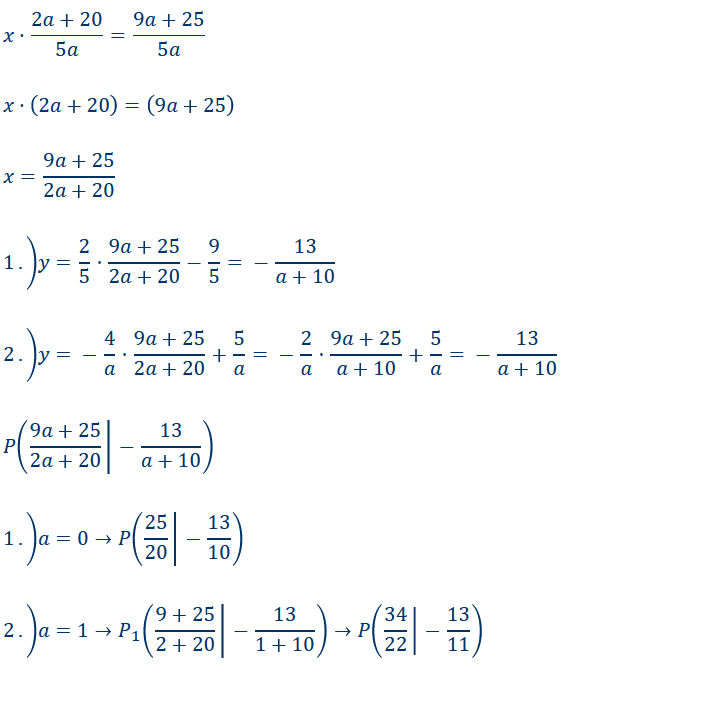
Text erkannt:
\( x \cdot \frac{2 a+20}{5 a}=\frac{9 a+25}{5 a} \)
\( x \cdot(2 a+20)=(9 a+25) \)
\( x=\frac{9 a+25}{2 a+20} \)
1.) \( y=\frac{2}{5} \cdot \frac{9 a+25}{2 a+20}-\frac{9}{5}=-\frac{13}{a+10} \)
2.) \( y=-\frac{4}{a} \cdot \frac{9 a+25}{2 a+20}+\frac{5}{a}=-\frac{2}{a} \cdot \frac{9 a+25}{a+10}+\frac{5}{a}=-\frac{13}{a+10} \)
\( P\left(\frac{9 a+25}{2 a+20} \mid-\frac{13}{a+10}\right) \)
1. \( a=0 \rightarrow P\left(\frac{25}{20} \mid-\frac{13}{10}\right) \)
2.) \( a=1 \rightarrow P_{1}\left(\frac{9+25}{2+20} \mid-\frac{13}{1+10}\right) \rightarrow P\left(\frac{34}{22} \mid-\frac{13}{11}\right) \)