Multiplikatormethode nach Lagrange - achsenparalleles REchteck mit max. Umfang - Eckpunkte?

Question

Aufgabe:

Schreiben Sie dem Einheitskreises unter Verwendung der Multiplikatormethode nach
Lagrange ein achsenparalleles Rechteck mit maximalem Umfang ein. Wie lauten dessen
Eckpunkte?

Problem/Ansatz:

Weiß jemand, wie man dieses Beispiel lösen könnte?

Answer 1

Aloha :)

Wir betrachten einen Punkt \((x|y)\) im ersten Quadranten des Koordinatensystems, d.h. \(x\ge0\) und \(y\ge0\). Da er auf dem Einheitskreis liegen soll, gehorcht er der Randbedingung \(x^2+y^2\). Die Höhe des beschriebenen Rechtecks ist dann \(2y\) und die Breite \(2x\). Damit ist die Fläche \(4xy\).$$F(x;y)=4xy\to\text{Max!}\quad;\quad g(x;y)=x^2+y^2\stackrel!=1\quad;\quad x,y\ge0$$

Nach Lagrange muss der Gradient der zu optimierenden Funktion proportional zum Gradienten der Nebenbedingung sein:$$\operatorname{grad}F(x;y)=\lambda\cdot\operatorname{grad}g(x;y)\quad\implies\quad\binom{4y}{4x}=\lambda\binom{2x}{2y}\quad\implies\quad$$$$\frac{4y}{4x}=\frac{\lambda\cdot2x}{\lambda\cdot2y}=\frac{x}{y}\quad\implies\quad \frac{4y\cdot y}{4x\cdot y}=\frac{4x\cdot x}{4x\cdot y}\quad\implies\quad y^2=x^2\quad\implies\quad x=y$$Da wir oben vereinbart haben, den Punkt im ersten Quadranten zu suchen, brauchen wir beim Wurzelziehen nur die positiven Werte zu beachten. Wir setzen unsere Erkenntnis in die Nebenbedingung ein:$$1\stackrel!=x^2+y^2=x^2+x^2=2x^2\implies x^2=\frac{1}{2}\implies x=\frac{1}{\sqrt2}\implies y=x=\frac{1}{\sqrt2}$$

Das Rechteck ist also ein Quadrat und die 4 gesuchten Eckpunkte lauten wegen der Symmetrie:

$$\left(\frac{1}{\sqrt2}\bigg|\frac{1}{\sqrt2}\right)\quad;\quad\left(\frac{-1}{\sqrt2}\bigg|\frac{1}{\sqrt2}\right)\quad;\quad\left(\frac{-1}{\sqrt2}\bigg|\frac{-1}{\sqrt2}\right)\quad;\quad\left(\frac{1}{\sqrt2}\bigg|\frac{-1}{\sqrt2}\right)$$

~plot~ {1/sqrt(2)|1/sqrt(2)} ; {-1/sqrt(2)|1/sqrt(2)} ; {-1/sqrt(2)|-1/sqrt(2)} ; {1/sqrt(2)|-1/sqrt(2)} ; sqrt(1-x^2) ; -sqrt(1-x^2) ; [[-1,5|1,5|-1|1]] ~plot~

Answer 2

Ja, durch eine Zeichnung! das Rechteck hat die Seiten 2x und 2y, also die Flache?

die Nebenbedingung ist x^2+y^2=1

oder du rechnest mit Polarkoordinaten , dann ist die Nebenbedingung einfacher r=1 x=cos(t), y=sin(t)

aber das ist wohl zu einfach und ohne Lagrange.

lul

Answer 3

Hallo Antonia,

der Umfang eines Rechtecks ist \(U=2(a+b)\). Liegen alle vier Eckpunkte auf dem Einheitskreis und bezeichnen wir die Koordinaten des Eckpunktes \(C\) im 1.Quadraten mit \(x\) und \(y\), ...

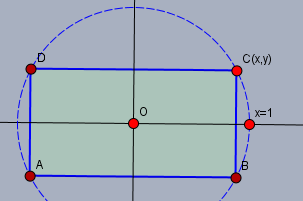
...so hat das achsenparallele Rechteck den Umfang$$U=2(2x+2y) = 4x+4y$$Dieser Wert soll maximiert werden, das ist unsere Hauptbedingung.

Wenn man sich \(U\) als Funktionswert über einer Ebene vorstellt, so stellt die Funktion \(U(x,y)\) selbst ebenso eine Ebene dar. Die sieht so aus:

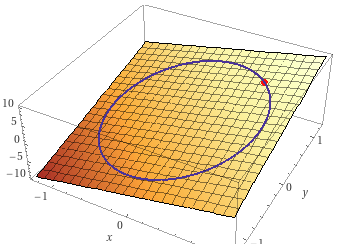
Du siehst das die Ebene zu positiven Werten von \(x\) und \(y\) hin ansteigt, d.h. der Umfang wird dort immer größer. Die Nebenbedingung besagt nun aber, dass unser Eckpunkt \(C\) auf dem Einheitskeis liegen soll, der oben in der Ebene eingezeichnet ist. Wir suchen also den höchsten Punkt auf dem blauen Kreis.

Lagrange sagt nun, dass eine Eigenschaft eines Maximums (und auch Minimums) darin besteht, dass dort die 'Höhenlinien' von Haupt- und Nebenbedingung parallel verlaufen. Die 'Höhenlinien' einer Funktion ist die Kurve mit gleichem Funktionswert und diese steht immer senkrecht auf der Richtung des stärksten Anstiegs. Und den wiederum bekommt man über die Richtung der Ableitung.

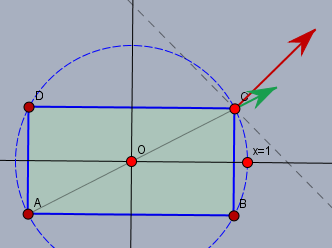
Die schwarze gestrichelte Gerade ist die 'Höhenlinie' von \(U(x,y)\). D.h. mit einem Eckpunkt auf dieser Geraden hätte jedes Rechteck den selben Umfang. Der rote Pfeil steht senkrecht dazu und zeigt in Richtung des stärksten Anstiegs; das lässt sich berechnen:$$U= 4x+4y \\ \frac{\partial U}{\partial x} = 4, \quad \frac{\partial U}{\partial y} = 4\\ \implies \text{grad}\,U(x,y) = \begin{pmatrix} 4\\4 \end{pmatrix}$$Für die Nebenbedingung gilt, dass ihre 'Höhenlinie' auf dem Einheitskreis liegen. Ist ja auch klar, denn das ...$$N(x,y) = x^2+y^2-1$$.. ist ja auch genau die Nebenbedingung. Ihre Ableitung (der grüne Pfeil) sieht so aus$$N(x,y) = x^2+ y^2 -1 \\ \frac{\partial N}{\partial x} = 2x, \quad \frac{\partial N}{\partial y} = 2y\\\implies \text{grad}\,N(x,y) = \begin{pmatrix} 2x\\2y \end{pmatrix}$$und steht immer senkrecht auf dem Kreis. Und wenn nun die Höhenlinien parallel laufen, dann müssen auch die Richtungen des stärksten Anstiegs im Maximum parallel laufen und damit muss es einen Wert \(\lambda \in \mathbb{R}\) geben ...$$\text{grad}\,U(x,y) + \lambda \cdot \text{grad}\,N(x,y) = \vec 0$$... der beide Richtungen in einander überführt.

Ohne Rechnung lässt sich hier bereits sagen, dass dies offensichtlich der Fall ist, wenn \(C(x,y)\) auf der Winkelhalbierenden der Koordinatenachsen liegt, also \(x=y\) gilt. Die vollständige Rechnung besteht darin, zunächst die sogenannte Lagrange-Funktion auf zustellen$$L(x,y,\lambda) = U(x,y) + \lambda \cdot N(x,y) \\ \phantom{L(x,y,\lambda) }= 4x+4y + \lambda(x^2+y^2-1)$$und dies dann nach den Koordinaten \(x\) und \(y\) abzuleiten und zu 0 zu setzen$$\frac{\partial L}{\partial x} = 4 + 2\lambda x = 0\\ \frac{\partial L}{\partial y} = 4 + 2\lambda y=0 \\ \implies x=y$$Einsetzen in die Nebenbedingung gibt dann die konkreten Werte \(x=y= \frac 12 \sqrt 2\) (die negativen Werte entfallen). Streng genommen sollte man nun noch prüfen, ob es sich auch um ein Maximum und kein Minimum handelt. Dies ist hier aber offensichtlich der Fall.

Gruß Werner