Aufgabe:
Pr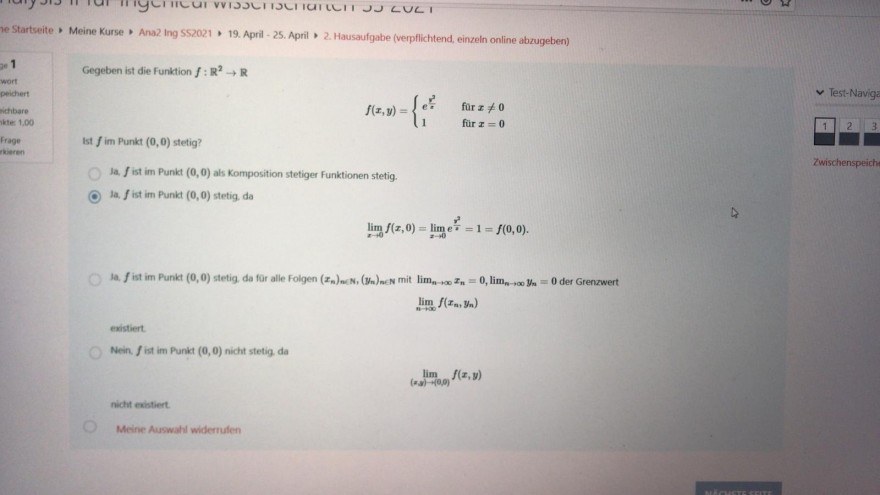
Text erkannt:
Gegeben ist die funktion \( f: \mathbb{R}^{2} \rightarrow \mathbb{R} \)
$$ f(x, y)=\left\{\begin{array}{ll} e^{2} & \text { fur } x \neq 0 \\ 1 & \text { für } x=0 \end{array}\right. $$
ist \( f \) im Punkt \( (0,0) \) stetig?
la. \( f \) ist im Punkt \( (0,0) \) als Komposition stetiger funktionen stetig.
Ia. \( f \) ist im Punkt \( (0,0) \) stetig da
$$ \lim \limits_{x \rightarrow 0} f(x, 0)=\lim \limits_{z \rightarrow 0} e^{\frac{\overrightarrow{2}}{7}}=1=f(0,0) $$
\( \lim \limits_{n \rightarrow \infty} f\left(x_{n}, y_{n}\right) \)
existiert.
Nein \( f \) is im Punit \( (0,0) \) nicht stetig da
$$ \lim \limits_{\left(x_{s}\right) \rightarrow(e, q)} f(x, y) $$
nictut ewitiert.
Meine Auswahl widernien
oblem/Ansatz: Ist diese Antwortmöglichkeit richtig? wenn ich für x eine folge nehme, welche gegen 0 konvergiert dann habe ich ja: lim xn->unendlich g(xn, yn) also kriege ich dann bei der aufgabe, wenn ich den limes rechne e^(y/0) was ja unendlich wäre...