
Text erkannt:
2.1 Rekonstruktion eines Bestandes aus Änderungsraten
Ein leeres Wasserbecken hat einen Zufluss und einen Abfluss. Zunächst wird der Zufluss \( 15 \mathrm{~min} \) geöffnet. Die Zuflussgeschwindigkeit beträgt \( 300 \frac{1}{\min } \). Dann wird 20 min lang der Zufluss geschlossen und der Abfluss geöffnet. Die Abflussgeschwindigkeit beträgt \( 100 \frac{1}{\min } \).
(1) Zeichnen Sie den Graphen der Funktion f: Zeitdauer (in min) \( \rightarrow \) Zuflussgeschwindigkeit (in \( \frac{1}{\min } \) ). Deuten Sie dabei die Abflussgeschwindigkeit als negative Zuflussgeschwindigkeit.
(2) Ermitteln Sie, wie viel Liter sich nach \( 5,10,15,20,25,30,35 \) min im Becken befinden. Zeichnen Sie den Graphen der Funktion \( \mathrm{F} \), die die Wassermenge im Becken in Abhängigkeit von der Zeit beschreibt.
(3) Berechnen Sie den Flächeninhalt der einzelnen Rechtecke zwischen dem Graphen der Funktion \( f \) und der \( x \) -Achse über dem Intervall \( [0 ; 35] \). Untersuchen Sie, welcher Zusammenhang mit den Funktionswerten von \( \mathrm{F} \) besteht.
Aufgabe: Hier ist meine erste Idee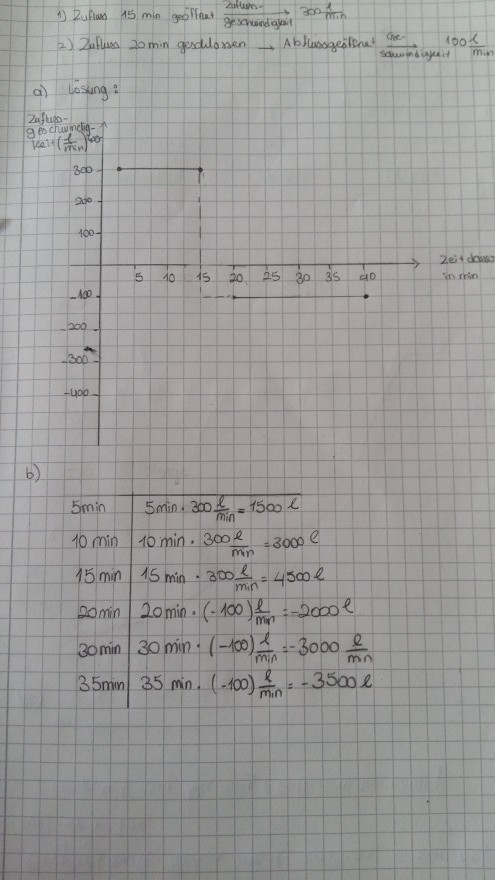
…
Problem/Ansatz:
Ich weiß es nicht wie ich den Graph zu b) zeichnen kann. Soll ich genauso vorgehen wie a)?
Auch bei Nr. 3 weiß ich die Lösung nicht.