Hallo,
bei dieser Konstruktionsaufgabe gibt es viele Wege zur Lösung. Im folgenden zeige ich einen Weg ohne Dreiteilung einer Strecke.
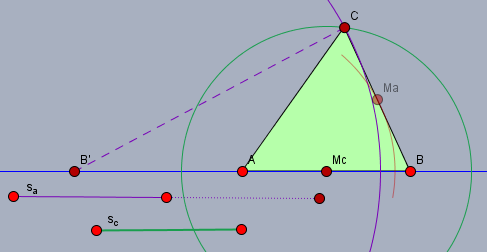
Zeichne eine Gerade (blau) und trage die Strecke \(c\) darauf ab. Die Endpunkte sind \(A\) (links) und \(B\). Halbiere diese Strecke. Der Mittelpunkt sei \(M_c\). Spiegele \(B\) an \(A\) zu \(B'\) (schlage einen Kreis mit \(|AB|\) um \(A\)).
Nun ziehe einen Kreis (lila) mit dem Radius der doppelten Strecke \(s_a\) (lila gestrichelt) um \(B'\) und einen weiteren Kreis (grün) mit dem Radius \(s_c\) um \(M_c\). Beide Kreise schneiden sich oberhalb von \(c\) im Punkt \(C\).
Das Dreieck \(\triangle ABC\) ist das gesuchte Dreieck.
Diskutieren Sie, ob ein solches Dreieck immer konstruierbar ist
Das ist genau dann konstruierbar, wenn der Schnittpunkt \(C\) der beiden Kreise existiert. Also wenn diese beiden Kreise sich auch schneiden. Welche Bedingungen dazu erfüllt sein müssen, kann man aus der Konstruktion ablesen ;-)
[spoiler]
Die Bedingung für die Konstruierbarkeit des oben beschriebenen Dreiecks ist $$2s_a - s_c \lt \frac 32c \lt 2s_a + s_c$$
[/spoiler]
Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner
