Hallo Oli,
Für die Lösung dieser Aufgabe gibt es mehrere Möglichkeiten. Im Folgenden beschreibe ich eine davon.
Du weißt doch bereits, wie man die Strecke \((1+\sqrt 5)/2\) konstruiert. Das war die Strecke \(|CP|\) bei der Konstruktion der Strecke \((1+\sqrt 5)/4\). Die Zahl $$\phi = \frac 12(1+\sqrt 5)$$ ist das Teilungsverhältnis des Goldenen Schnitts. Beim regelmäßigen Fünfeck verhalten sich die Länge der Diagonalen zu den Länge der Seiten im Verhältnis \(\phi\). Und mit diesem Wissen kann man - aufbauend auf der letzten Konstruktion - eine Ecke eines regelmäßigen Fünfecks konstruieren.
Nutze die Konstruktion aus Deiner letzten Frage und schlage um \(C(1|\,0)\) einen Kreis (lila) mit Radius \(|CP|\), der den Kreis (grün) um \(A(0|\,0)\) mit Radius \(|AB|=1\) in \(P'\) scheidet.

Zeichne die Gerade \(a\) durch die Punkte \(AB\) und die Gerade \(e\) durch \(P'A\). Der Winkel \(\angle CAP'=\alpha\) (gelb) ist genau \(108°\) und somit der Innenwinkel eines regelmäßigen Fünfecks.
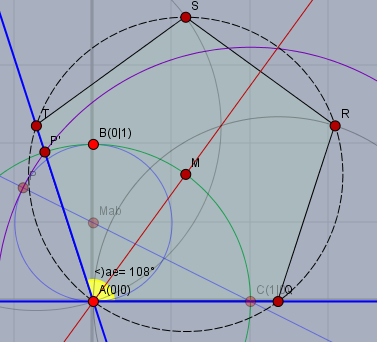
Für den Radius \(1\) konstruiere die Winkelhalbierende (rot) von \(\alpha\), die den Kreis (grün) um \(A\) oberhalb der Geraden \(a\) in \(M\) schneidet. \(M\) ist der Mittelpunkt des gesuchten Fünfecks. Der Kreis (schwarz gestrichelt) um \(M\) mit Radius \(|MA|=1\) schneidet \(a\) außer in \(A\) noch in \(Q\) und die Gerade \(e\) noch in \(T\).
Mit einem Kreis um \(Q\) mit Radius \(|AQ|\) kommt man zu \(R\) und mit einem Kreis um \(T\) mit Radius \(|TA|\) zum Punkt \(S\). Das Fünfeck \(AQRST\) ist das gesuchte Fünfeck.
Dann muss man noch die Korrektheit der Konstruktionsschritte beweisen/erklären.
Mit den Informationen, die ich Dir gegeben habe, solltest Du das schaffen. Falls Du trotzdem noch Fragen hast, so melde Dich bitte.
Gruß Werner