Tangentengleichung aufstellen schnittpunkt

Question

Aufgabe:

P=9 und q=6
In welchem Punkt \( \left(x_{0}, y_{0}\right) \) des Graphen von \( f(x)=\frac{q}{x} \) muss die Tangente angelegt werden, damit diese die X-Achse in x=p schneidet?
Wie lautet die Gleichung der Tangente?

Problem/Ansatz:

Hallo die Tangentengleichung lautet glaube ich ja : t(x)= y(x0)+y‘(x0)*(x-x0)

Mein f(x) ist 6/x

Und f‘(x) -6/x^2  wie gehe ich jetzt weiter vor habe t(9) berechnet, jedoch komme ich dort durcheinander. Beim x0 auflösen. Könnte jmabd helfen. Lieben dank im voraus

Answer 1

f ( x ) = 6 / x
f ´( x ) = - 6 / x^2
Eine symbolische Skizze

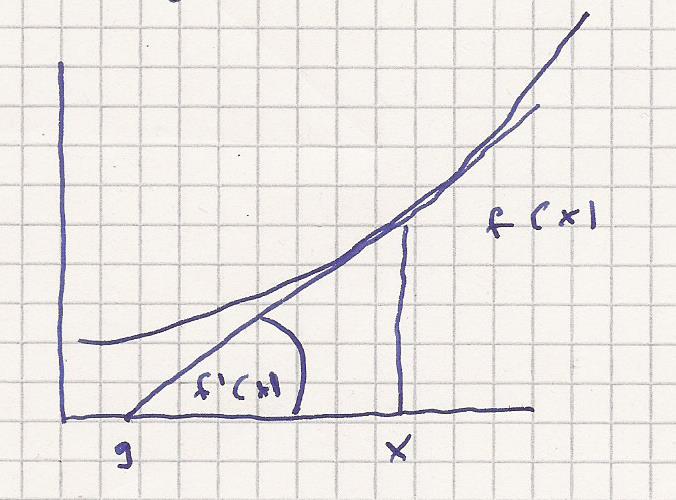
f´( x ) = f ( x ) / ( x - 9 )

- 6 / x^2 = ( 6 / x ) / ( x - 9 )

x = 9 / 2

f ´( 9/2 ) = - 6 / (9/2)^2 = - 8 / 27

Tangente
t ( x ) = - 8/27 * x + b
t ( 9 ) = - 8/27 * 9 + b = 0
b = 8/27 * 9 = 2  2/3

t ( x ) = - 8/27 * x + 2  2/3

mfg Georg

Comments

Meine Grafik sieht so aus

---

Ich versuche meine Lösung mal Hochzuladen als Bild

---

@Georg:

Wie kommst du auf -8/27?

---

Wie kommst du auf -8/27?

Es wurde die Ableitung an der Stelle 9/2 berechnet

f ´( 9/2 ) = - 6 / (9/2)^2 = - 8 / 27

Answer 2

f(x) = 6/x

f '(x) = -6/x^2

f(9) = 6/9 = 2/3

f '(9) = -6/81 = - 2/27

t(x)= (x-9)*(-2/27) +2/3 = -2/27*x+18/27 +2/3 = -2/27*x+ 36/27

Comments

Habe t(x)= -2/27x+10/9 raus habe es einfach mit t(x)=mx+b berechnet wäre es auch so korrekt?

Lg und danke

---

f(x) = mx*b

m= -2/27

f(9) = 2/3

2/3= -2/27*9 +b

b= 36/27 = 4/3

---

Zur Kontrolle deiner Lösung zeichne doch einfach einmal f und deine Tangente.

---

Achtung. Es ist nicht die Tangente an der Stelle x = 9 an den Graphen von f(x) gesucht sondern die Tangente an den Graphen, die eine Nullstelle bei x = 9 hat. Das ist eine andere Aufgabenstellung

Hier eine Skizze von dem was du berechnet hast

~plot~ 6/x;36/27-2/27*x;{9|2/3};{18|0};[[-1|20|-1|15]] ~plot~

Answer 3

f(x) = 6/x

f'(x) = - 6/x^2

Ansatz für den Tangentenpunkt

(f(x) - 0) / (x - 9) = f'(x) → x = 9/2

f(9/2) = 4/3

Ansatz für die Tangentengleichung

t(x) = f'(9/2)·(x - 9/2) + f(9/2) = 8/3 - 8/27·x

Skizze

~plot~  6/x;8/3-8/27x;{9/2|4/3};{9|0};[[-1|12|-1|9]] ~plot~

Comments

MMache ich ein Fehler? Ich setze in die erste Ableitung f'(9)=-6/9^2= -2/27  warum rechnen Sie 9/2? Vielen Dank an die zahlreichen antworten

---

Wenn du f'(9) berechnest dann ist das die Steigung an der Stelle x = 9. Du sollst aber keine Tangente an der Stelle x = 9 an den Graphen legen. Schau dir die Skizze an. Gesucht ist die Tangente, die die x-Achse bei x = 9 schneidet.

---

Vielen Dank habe es Verstanden✌