Extremwertaufgabe: Gesamtlänge möglichst gering halten

Question

Am Ufer eines Kanals soll eine Kläranlage X für die Fabriken R und W errichtet werden (Abmessungen siehe Abbildung).
1) In welcher Entfernung von A muss die Kläranlage errichtet werden, damit die Gesamtlänge der von den Fabriken zur Kläranlage führenden Abwasserkanäle möglichst gering ist?

Der Screenshot dient nur zur Hilfe, falls unerwünscht bitte löschen. danke!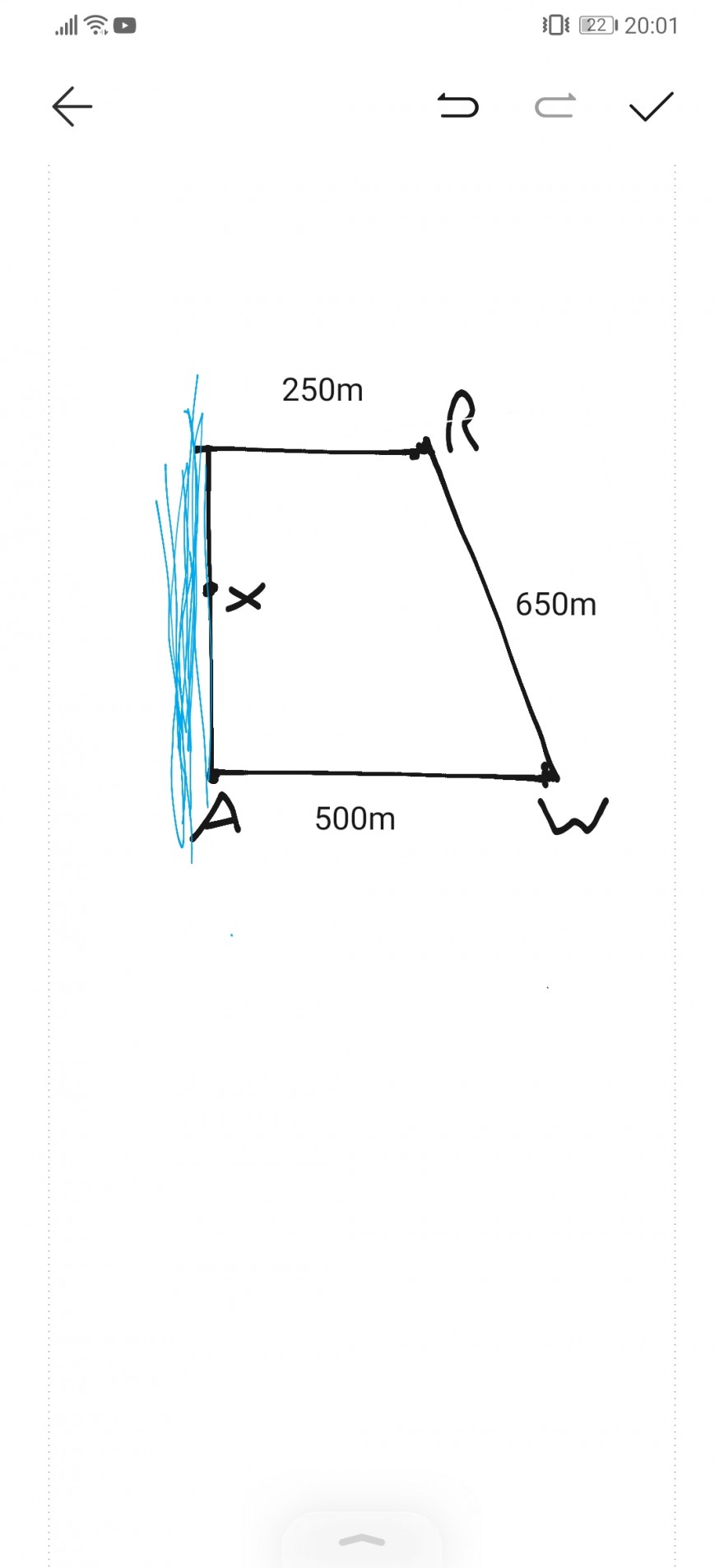

Text erkannt:

\( \leftarrow \quad \supset \subset \)

Answer 1

Bei mir sieht das wie folgt aus

Comments

Danke 400 ist richtig!

Answer 2

j^2=500^2+u^2               

i^2=250^2+(600-u)^2

\( j=\sqrt{500^{2}+u^{2}} \)
\( i=\sqrt{250^{2}+(600-u)^{2}} \)
\( d=i+j \) soll minimal werden.
\( d=\sqrt{500^{2}+u^{2}}+\sqrt{250^{2}+(600-u)^{2}} \)
\( d^{\cdot}=\frac{u}{\sqrt{500^{2}+u^{2}}}-\frac{(600-u)}{\sqrt{250^{2}+(600-u)^{2}}} \)
\( \frac{u}{\sqrt{500^{2}+u^{2}}}-\frac{(600-u)}{\sqrt{250^{2}+(600-u)^{2}}}=0 \)
\( u=400 \)

Comments

Habe versucht selber die Hauptbedingung und NB zu finden jedoch vergebens. Jetzt hab ich auch den Knoten gefunden. Danke ihr seids einfach spitze!