Aufgabe:
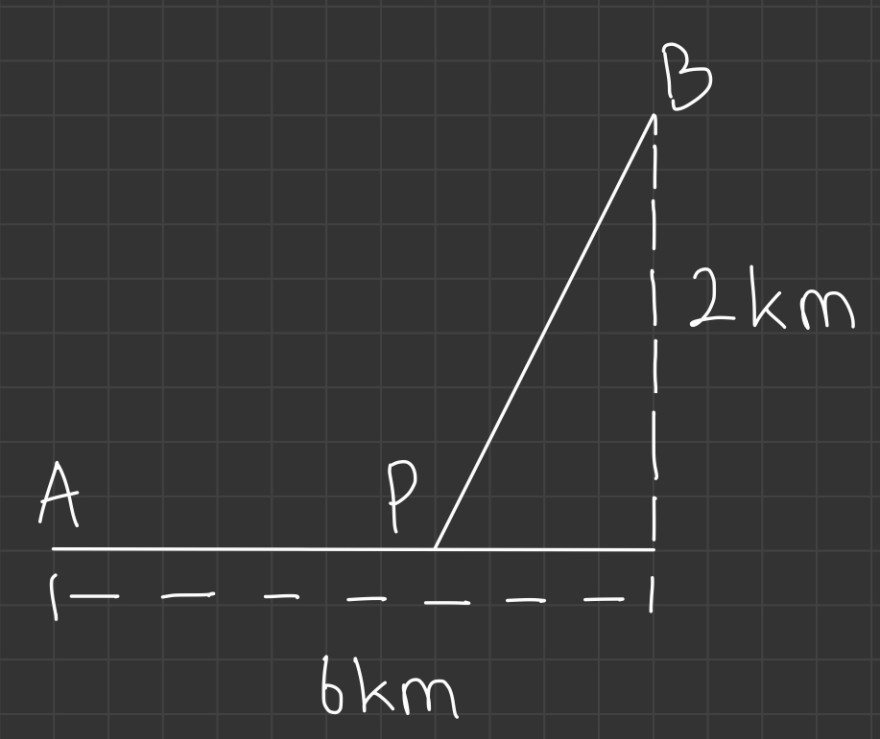
Ein Wanderer will von A nach B laufen, wobei er den Teilweg AP seines Weges auf einer gerade verlaufenden Straße gehen kann. Auf der Straße hält er eine Geschwindigkeit u1 = 6 km/h, auf dem Rest des Weges nur u2 = 4 km/h. An welcher Stelle muss er abbiegen, wenn er B möglichst schnell erreichen will?
Bei \(\frac{x}{6} + \sqrt{2^2 + (6-x)^2}\) komme ich überhaupt nicht weiter.
Würde mich über eine Lösung freuen :)