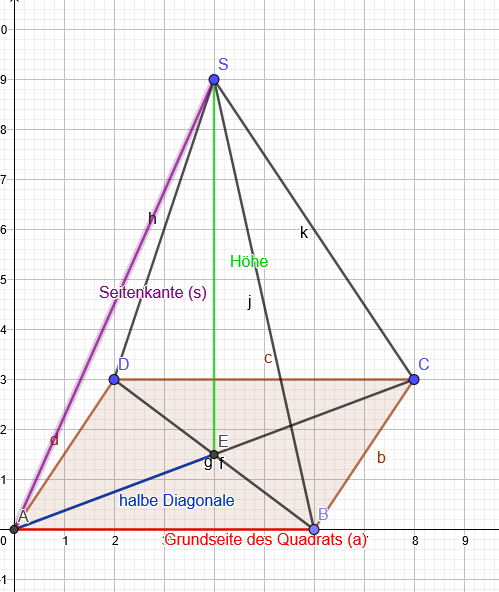
"Berechne die Größe der quadratischen Pyramide
gegeben ist s = 92,2 cm und h = 62,5 cm gesucht ist hier a"
Die Diagonale des Quadrats ist d=\( \sqrt{2a^2} \)=a\( \sqrt{2} \)
Rechtwinkliges Dreieck aus der halben Diagonale, der Höhe und der Seitenkante s:
s^2=(\( \frac{1}{2} \)*a\( \sqrt{2} \))^2+h^2=\( \frac{1}{4} \)*2a^2+h^2=\( \frac{1}{2} \)a^2+h^2
Nun nach a auflösen:
\( \frac{1}{2} \)a^2+h^2=s^2
a^2=2s^2-2h^2
a=\( \sqrt{2s^2-2h^2} \)
Nun die Werte für s und h einsetzen einsetzen.